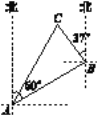جâؤ؟ؤعبف
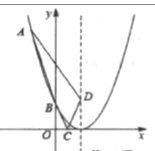
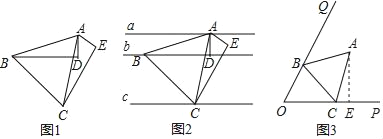
،¾جâؤ؟،؟£¨1£©بçح¼1£¬،÷AECضذ£¬،دE£½90،م£¬½«،÷AECبئµمAث³ت±صëذ×ھ60،مµأµ½،÷ADB£¬ACسëAB¶شس¦£¬AEسëAD¶شس¦
¢ظاëض¤أ÷،÷ABCخھµب±كب½اذخ£»
¢عبçح¼2£¬BDثùشعµؤض±دكخھb£¬·ض±ً¹µمA،¢C×÷ض±دكbµؤئ½ذذدكa،¢c£¬ض±دكa،¢bض®¼نµؤ¾àہëخھ2£¬ض±دكa،¢cض®¼نµؤ¾àہëخھ7£¬شٍµب±ك،÷ABCµؤ±ك³¤خھ،، ،،£®
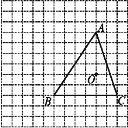
£¨2£©بçح¼3£¬،دPOQ£½60،م£¬،÷ABCخھµب±كب½اذخ£¬µمAخھ،دPOQؤع²؟ز»µم£¬µمB،¢C·ض±ًشعةندكOQ،¢OPةد£¬AE،حOPسعE£¬OE£½5£¬AE£½2![]() £¬اَ،÷ABCµؤ±ك³¤£®
£¬اَ،÷ABCµؤ±ك³¤£®
،¾´ً°¸،؟£¨1£©¢ظدê¼û½âخِ£»¢ع![]() £»£¨2£©
£»£¨2£©![]() .
.
،¾½âخِ،؟
£¨1£©سةذ×ھµؤذشضت؟ةµأ£؛AB£½AC£¬،دBAC£½60،م£¬¼´؟ةض¤،÷ABCخھµب±كب½اذخ£»
£¨2£©¹µمE×÷EG،حض±دكa£¬رس³¤GE½»ض±دكcسعµمH£¬؟ةµأGH£½7£¬AD£½2£¬سةذ×ھµؤذشضت؟ةµأAD£½AE£½2£¬،دDAE£½60،م£¬؟ةاَGE£½1£¬EH£½6£¬سةبٌ½اب½ا؛¯ت؟ةاَCE£½4![]() £¬¸ù¾ف¹´¹ة¶¨ہي؟ةاَµب±ك،÷ABCµؤ±كACµؤ³¤£»
£¬¸ù¾ف¹´¹ة¶¨ہي؟ةاَµب±ك،÷ABCµؤ±كACµؤ³¤£»
£¨3£©¹µمA×÷،دAHO£½60،م£¬½»OQسعµمG£¬½»OPسعµمH£¬¸ù¾فجطتâب½ا؛¯تضµ؟ةاَAH£½4£¬ح¨¹ض¤أ÷،÷OBC،ص،÷HCA£¬؟ةاَAH£½OC£½4£¬CE£½1£¬¸ù¾ف¹´¹ة¶¨ہي؟ةاَ،÷ABCµؤ±كACµؤ³¤£®
½â£؛£¨1£©،ك½«،÷AECبئµمAث³ت±صëذ×ھ60،مµأµ½،÷ADB£¬
،àAB£½AC£¬،دBAC£½60،م£¬
،à،÷ABCخھµب±كب½اذخ£®
£¨2£©¹µمE×÷EG،حض±دكa£¬رس³¤GE½»ض±دكcسعµمH£¬
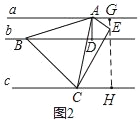
،كa،خb،خc£¬
،àEH،حض±دكc£¬
،كض±دكa،¢cض®¼نµؤ¾àہëخھ7£¬
،àGH£½7
،ك½«،÷AECبئµمAث³ت±صëذ×ھ60،مµأµ½،÷ADB£¬
،àAD£½AE£¬،دADB£½،دAEC£½90،م£¬،دDAE£½60،م£¬
،كض±دكa،¢bض®¼نµؤ¾àہëخھ2£¬
،àAD£½2£½AE£¬
،ك،دGAE£½،دGAD©پ،دDAE£½90،م©پ60،م£½30،م£¬
،àGE£½![]() AE£½1£¬،دAEG£½60،م£¬
AE£½1£¬،دAEG£½60،م£¬
،àEH£½7©پ1£½6£¬
،ك،دCEH£½180،م©پ،دAEC©پ،دAEG£¬
،à،دCEH£½30،م£¬
،àcos،دCEH£½![]() £¬
£¬
،àCE£½4![]()
شعRt،÷ACEضذ£¬AC£½![]() £½
£½![]() £½2
£½2![]() £¬
£¬
¹ت´ً°¸خھ£؛2![]()
£¨3£©¹µمA×÷،دAHO£½60،م£¬½»OQسعµمG£¬½»OPسعµمH£¬
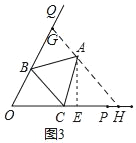
،كAE،حOP£¬،دAHO£½60،م
،àsin،دAHO£½![]()
،àAH£½4
،ك،÷ABCتاµب±كب½اذخ£¬
،àAB£½AC£½BC£¬،دACB£½60،م£½،دPOQ£¬
،ك،دPOQ+،دOBC+،دOCB£½180،م£¬،دACB+،دOCB+،دACH£½180،م£¬
،à،دACH£½،دOBC£¬ازBC£½AC£¬،دO£½،دAHC£½60،م£¬
،à،÷OBC،ص،÷HCA£¨AAS£©
،àAH£½OC£½4£¬
،àCE£½OE©پOC£½5©پ4£½1£¬
شعRt،÷ACEضذ£¬AC£½![]() £½
£½![]() £½
£½![]() £¬
£¬
،à،÷ABCµؤ±ك³¤خھ![]() £®
£®