题目内容
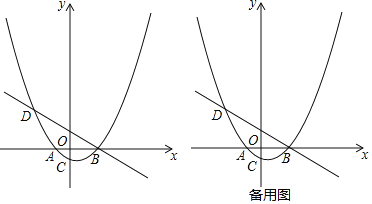
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2;
的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2;
(1)求反比例函数的表达式;
(2)根据图象直接写出﹣![]() x>
x>![]() 的解集;
的解集;
(3)将直线l1:y=- ![]() x沿y向上平移后的直线l2与反比例函数y=
x沿y向上平移后的直线l2与反比例函数y=![]() 在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.

【答案】(1) y=﹣![]() ;(2) x<﹣4 或 0<x<4;(3) y=-
;(2) x<﹣4 或 0<x<4;(3) y=-![]() .
.
【解析】
(1)直线l1:y= -![]() x经过点A,且A点的纵坐标是2,可得A(-4,2),代入反比例函数解析式可得k的值;(2)根据图象得到点B的坐标,进而直接得到﹣
x经过点A,且A点的纵坐标是2,可得A(-4,2),代入反比例函数解析式可得k的值;(2)根据图象得到点B的坐标,进而直接得到﹣ ![]() x>
x> ![]() 的解集即可;(3)设平移后的直线
的解集即可;(3)设平移后的直线 ![]() 与 x 轴交于点 D,连接 AD,BD,由平行线的性质可得出S△ABC=S△ABF,即可得出关于OD的一元一次方程,解方程即可得出结论.
与 x 轴交于点 D,连接 AD,BD,由平行线的性质可得出S△ABC=S△ABF,即可得出关于OD的一元一次方程,解方程即可得出结论.
(1)∵直线 l1:y=﹣![]() x 经过点 A,A 点的纵坐标是 2,
x 经过点 A,A 点的纵坐标是 2,
∴当 y=2 时,x=﹣4,
∴A(﹣4,2),
∵反比例函数 y=![]() 的图象经过点 A,
的图象经过点 A,
∴k=﹣4×2=﹣8,
∴反比例函数的表达式为 y=﹣![]() ;
;
(2)∵直线 l1:y=﹣![]() x 与反比例函数 y=
x 与反比例函数 y=![]() 的图象交于 A,B 两点,
的图象交于 A,B 两点,
∴B(4,﹣2),
∴不等式﹣ ![]() x>
x> ![]() 的解集为 x<﹣4 或 0<x<4;
的解集为 x<﹣4 或 0<x<4;
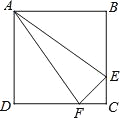
(3)如图,设平移后的直线 ![]() 与 x 轴交于点 D,连接 AD,BD,
与 x 轴交于点 D,连接 AD,BD,
∵CD∥AB,
∴△ABC 的面积与△ABD 的面积相等,
∵△ABC 的面积为 30,
∴S△AOD+S△BOD=30,即 ![]() OD(|yA|+|yB|)=30,
OD(|yA|+|yB|)=30,
∴![]() ×OD×4=30,
×OD×4=30,
∴OD=15,
∴D(15,0),
设平移后的直线 ![]() 的函数表达式为 y=﹣
的函数表达式为 y=﹣![]() x+b, 把 D(15,0)代入,可得 0=﹣
x+b, 把 D(15,0)代入,可得 0=﹣![]() ×15+b,
×15+b,
解得 b=![]() ,
,
∴平移后的直线![]() 的函数表达式为 y=-
的函数表达式为 y=-![]() .
.