题目内容
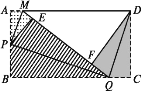
【题目】如图,矩形纸片ABCD,P是AB的中点,Q是BC上一动点,△BPQ沿PQ折叠,点B落在点E处,延长QE交AD于M点,连接PM.
(1)求证:△PAM≌△PEM;
(2)当DQ⊥PQ时,将△CQD沿DQ折叠,点C落在线段EQ上点F处.
①求证:△PAM∽△DCQ;
②如果AM=1,sin∠DMF=![]() ,求AB的长.
,求AB的长.
【答案】(1)见解析;(2)①见解析,②6
【解析】
(1)由矩形的性质及折叠的性质可得PE=PB,∠PEM=∠B=90°,由P点为AB中点可得PA=PB=PE,因为有公共边PM,所以利用HL即可证明△PAM≌△PEM;(2)①由(1)可得∠APM=∠EPM,根据折叠性质可得∠EPQ=∠BPQ,由∠B=90°,DQ⊥PQ可得∠BPQ+∠PQB=90°,∠PQB+∠DQC=180°-∠PQD=90°.进而可证明∠AMP=∠DQC,即可证明△PAM∽△DCQ;②设AP=x,则BP=AP=EP=x,AB=DC=2x,根据△AMP∽△BPQ可得BQ=x2,根据△AMP∽△CQD得CQ=2,进而可得AD=x2+2,根据sin∠DMF=![]() 列方程即可求出x的值,根据AB=2AP即可得答案.
列方程即可求出x的值,根据AB=2AP即可得答案.
(1)∵四边形ABCD是矩形,
∴∠A=∠B=90°,根据折叠的性质可知:PE=PB,∠PEM=∠B=90°;
∵P点为AB中点,
∴PA=PB=PE.
又∵PM=PM,
∴△PAM≌△PEM.
(2)①由(1)知△PAM≌△PEM,
∴∠APM=∠EPM.
根据折叠的性质可知:∠EPQ=∠BPQ,
∴∠APM+∠BPQ=∠EPM+∠EPQ=90°,
∵∠APM+∠AMP=90°,
∴∠BPQ=∠AMP,
∵∠B=90°,DQ⊥PQ,
∴∠BPQ+∠PQB=90°,∠PQB+∠DQC=180°-∠PQD=90°.
∴∠BPQ=∠DQC,
∴∠AMP=∠DQC.
又∵∠A=∠C=90°,
∴△AMP∽△CQD.
②设AP=x,则BP=AP=EP=x,AB=DC=2x,
∵由①知∠BPQ=∠AMP,∠A=∠B=90°,
∴△AMP∽△BPQ.
∴![]() ,即BQ=x2.
,即BQ=x2.
由△AMP∽△CQD得:![]() ,即CQ=2.
,即CQ=2.
AD=BC=BQ+CQ=x2+2.
∵在Rt△FDM中,sin∠DMF=![]() ,DF=DC=2x,
,DF=DC=2x,
∴![]() ,
,
变形得:3x2-10x+3=0,
解方程得:x1=3,x2=![]() (不合题意,舍去)
(不合题意,舍去)
∴AB=2x=6.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案