题目内容
【题目】等边三角形的内切圆半径、外接圆半径和高的比为（ ）
A. 3：2：1 B. 1：2：3 C. 2：3：1 D. 3：1：2
【答案】B
【解析】
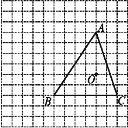
如图，⊙O 为△ABC 的内切圆，设⊙O 的半径为 r，作 AH⊥BC 于 H，利用等边三角形的性质得 AH 平分∠BAC，则可判断点 O 在 AH 上，所以 OH＝r，连接 OB，再证明
OA＝OB＝2r，则 AH＝3r，所以 OH：OA：AH＝1：2：3．
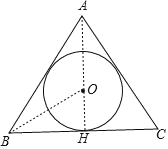
解： 如图，⊙O 为△ABC 的内切圆，设⊙O 的半径为 r，作 AH⊥BC 于 H，
∵△ABC 为等边三角形，
∴AH 平分∠BAC，即∠BAH＝30°，
∴点 O 在 AH 上，
∴OH＝r， 连接 OB，
∵⊙O 为△ABC 的内切圆，
∴∠ABO＝∠CBO＝30°，
∴OA＝OB，
在 Rt△OBH 中，OB＝2OH＝2r，
∴AH＝2r+r＝3r，
∴OH：OA：AH＝1：2：3，
即等边三角形的内切圆半径、外接圆半径和高的比为 1：2：3．
故选：B．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
【题目】小明同学三次到某超市购买A、B两种商品，其中仅有一次是有折扣的，购买数量及消费金额如下表：
类别 次数 | 购买A商品数量（件） | 购买B商品数量（件） | 消费金额（元） |
第一次 | 4 | 5 | 320 |
第二次 | 2 | 6 | 300 |
第三次 | 5 | 7 | 258 |
解答下列问题：
（1）第 次购买有折扣；
（2）求A、B两种商品的原价；
（3）若购买A、B两种商品的折扣数相同，求折扣数；
（4）小明同学再次购买A、B两种商品共10件，在（3）中折扣数的前提下，消费金额不超过200元，求至少购买A商品多少件．
