Question

【题目】如图，抛物线C1：y1=﹣2x2+4x+2与C2：y2=﹣x2+mx+n的顶点相同”．

（1）求抛物线C2的解析式.

（2）点A是抛物线C2上在第一象限的动点，过A作AQ⊥x轴，Q为垂足，求AQ+OQ的最大值．

Answer 1

【答案】（1）y2=﹣x2+2x+3；（2）

【解析】

（1）先求得y1顶点坐标，然后依据两个抛物线的顶点坐标相同可求得m、n的值；

（2）设A（a，-a2+2a+3）．则OQ=x，AQ=-a2+2a+3，然后得到OQ+AQ与a的函数关系式，最后依据配方法可求得OQ+AQ的最值．

（1）∵y1=﹣2x2+4x+2=﹣﹣2（x﹣1）2+4，

∴抛物线C1的顶点坐标为（1，4），

∵抛物线C1：与C2顶点相同，

∴=1，﹣1+m+n=4，

解得：m=2，n=3，

∴抛物线C2的解析式为y2=﹣x2+2x+3；

（2）如图1所示：

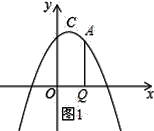
设点A的坐标为（a，﹣a2+2a+3），

∵AQ=﹣a2+2a+3，OQ=a，

∴AQ+OQ=﹣a2+2a+3+a=﹣a2+3a+3=﹣（a﹣）2+ ，

∴当a=时，AQ+OQ有最大值，最大值为．