��Ŀ����
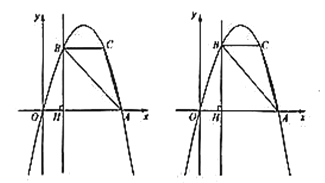
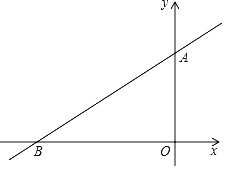
����Ŀ����ͼ���ھ���![]() �У�
��![]() .����
.����![]() �ӵ�
�ӵ�![]() ��������
��������![]() ��ÿ��4����λ���ȵ��ٶ����յ�
��ÿ��4����λ���ȵ��ٶ����յ�![]() �˶�.����
�˶�.����![]() �������
�������![]() ��
��![]() �غϣ���
�غϣ���![]() ����
����![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ��������������
��������������![]() .���
.���![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ![]() ��.
��.
��1����![]() _________________��
_________________��
�ڵ���![]() ��
��![]() ��ʱ���ú�
��ʱ���ú�![]() �Ĵ���ʽֱ�ӱ�ʾ�߶�
�Ĵ���ʽֱ�ӱ�ʾ�߶�![]() �ij�.
�ij�.
��2������![]() ���
���![]() �غ�ʱ����
�غ�ʱ����![]() ��ֵ��
��ֵ��
��3����������![]() ���ܳ�Ϊ
���ܳ�Ϊ![]() ����
����![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��4��ֱ��д���Խ���![]() ���ڵ�ֱ�߽�������
���ڵ�ֱ�߽�������![]() �ֳ�������ͼ�ε������Ϊ1��2ʱ
�ֳ�������ͼ�ε������Ϊ1��2ʱ![]() ��ֵ.
��ֵ.
���𰸡���1����15����![]() ����2��t��
����2��t��![]() ����3��
����3��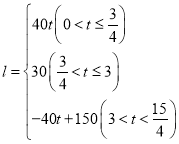 ����4��
����4��![]() ��
��![]() .
.
��������
��1�����ɾ��ε����ʺ��ɶ������ɵó������
����֤����APF�ס�ADC���ɵ�![]() ����һ�����ɵó������
����һ�����ɵó������
��2������F���D�غ�ʱ����ͼ1��֤����APD�ס�ADC���ó�![]() ����һ��������ý����
����һ��������ý����
��3����������ۣ�
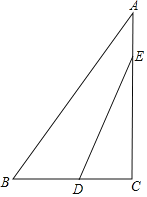
����0��t��![]() ʱ����ͼ2��ʾ���ɣ�1�����ã�PF��8t��ͬ���ɵã�PE��t�Ĺ�ϵ���Ӷ��ɵ�EF��t�Ĺ�ϵ�������ɵý����
ʱ����ͼ2��ʾ���ɣ�1�����ã�PF��8t��ͬ���ɵã�PE��t�Ĺ�ϵ���Ӷ��ɵ�EF��t�Ĺ�ϵ�������ɵý����
����![]() ��t��3ʱ����ͼ3��ʾ����ʱEF�ij���ͼ1�е�F��D�غ�ʱDE�ij���ȣ������ʱEF�ij����ɵó������
��t��3ʱ����ͼ3��ʾ����ʱEF�ij���ͼ1�е�F��D�غ�ʱDE�ij���ȣ������ʱEF�ij����ɵó������
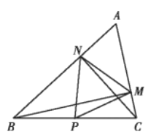
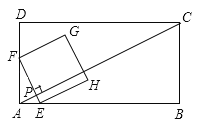
����3��t��![]() ʱ����ͼ4��ʾ��ͬ��1�����ã���CPF�ס�ABC�ס�EPC��Ȼ���������������ε����ʼ��ɵó�PF��PE��t�Ĺ�ϵ�������ɵ�EF��t�Ĺ�ϵʽ�����⼴�ý����
ʱ����ͼ4��ʾ��ͬ��1�����ã���CPF�ס�ABC�ס�EPC��Ȼ���������������ε����ʼ��ɵó�PF��PE��t�Ĺ�ϵ�������ɵ�EF��t�Ĺ�ϵʽ�����⼴�ý����
��4���ɣ�2�����֪���Խ���AC���ڵ�ֱ�߽�������EFGH�ֳ�������ͼ�ε������Ϊ1��2ʱ��ֻ����ͼ3�п��ܳ��֣��ٷ�PE��PF��1��2��PF��PE��1��2����������������������ε����ʺ�ͼ3�Ľ��ۣ�EF=10������⼴�ɣ�
�⣺��1�������ı���ABCD�Ǿ��Σ����B��90�㣬
��AC��![]() ��
��
�ʴ�Ϊ��15��
�����ı���ABCD�Ǿ��Σ����D��90�㣬AD��BC��3![]() ��CD��AB��6
��CD��AB��6![]() ��
��
��EF��AC�����APF��90�㣽��D��
�ߡ�PAF����DAC�����APF�ס�ADC��
��![]() ����
����![]() ����ã�PF��8t��
����ã�PF��8t��
��2������F���D�غ�ʱ����ͼ1��ʾ��
�ߡ�APD����ADC��90�㣬��PAD����DAC��
���APD�ס�ADC��
��![]() ����
����![]() ��
��
��ã�t��![]() ��
��
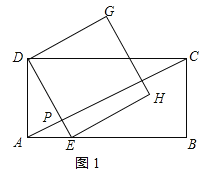
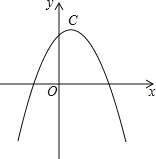
��3������0��t��![]() ʱ����ͼ2��ʾ��
ʱ����ͼ2��ʾ��
�ɣ�1�����ã�PF��8t��ͬ������ã�PE��2t����EF��10t��
��l��4EF��40t��
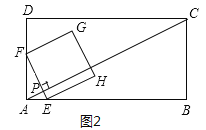
����![]() ��t��3ʱ����ͼ3��ʾ����ʱEF�ij���ͼ1�е�F��D�غ�ʱDE�ij���ȣ�
��t��3ʱ����ͼ3��ʾ����ʱEF�ij���ͼ1�е�F��D�غ�ʱDE�ij���ȣ�
��EF��10t��![]() ����l��4��
����l��4��![]() ��30��
��30��
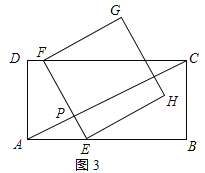
����3��t��![]() ʱ����ͼ4��ʾ��ͬ��1�����ã���CPF�ס�ABC�ס�EPC��
ʱ����ͼ4��ʾ��ͬ��1�����ã���CPF�ס�ABC�ס�EPC��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��
��ã�PF��![]() ��15��4t����PE��2��15��4t����
��15��4t����PE��2��15��4t����
��EF��PF+PE��![]() ��15��4t����
��15��4t����
��l��4��![]() ��15��4t������40t+150��
��15��4t������40t+150��
���ϣ�![]() ��
��![]() ֮��ĺ�����ϵʽ�ǣ�
֮��ĺ�����ϵʽ�ǣ�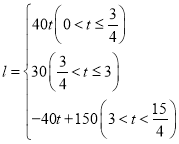 ��
��
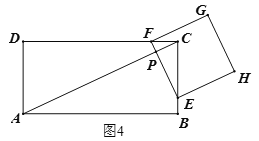
��4���ɣ�2�����֪���Խ���AC���ڵ�ֱ�߽�������EFGH�ֳ�������ͼ�ε������Ϊ1��2ʱ��ֻ����ͼ3�п��ܳ��֣���PE��PF��1��2����PF��PE��1��2��
��PE��PF��1��2ʱ����EF��![]() ����PF��
����PF��![]() EF��5��
EF��5��
�ߡ�CPF�ס�CDA����![]() ����
����![]() ����ã�PF��
����ã�PF��![]() ��15��4t����
��15��4t����
��![]() ��15��4t����5����ã�t��
��15��4t����5����ã�t��![]() ��
��

��PF��PE��1��2ʱ��PF��![]() EF��
EF��![]() ����
����![]() ��15��4t����
��15��4t����![]() ����ã�t��
����ã�t��![]() ��
��
�����������Խ���AC���ڵ�ֱ�߽�������EFGH�ֳ�������ͼ�ε������Ϊ1��2ʱt��ֵΪ![]() ��
��![]() ��
��