ЬтФПФкШн
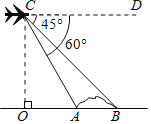
ЁОЬтФПЁПЖЈвхЃКНЋКЏЪ§CЕФЭМЯѓШЦЕуPЃЈ0ЃЌnЃЉа§зЊ180ЁуЃЌЕУЕНаТЕФКЏЪ§C1ЕФЭМЯѓЃЌЮвУЧГЦКЏЪ§C1ЪЧКЏЪ§CЙигкЕуPЕФЯрЙиКЏЪ§ЃЎ
Р§ШчЃКЕБnЃН1ЪБЃЌКЏЪ§![]() ЙигкЕуPЃЈ0ЃЌ1ЃЉЕФЯрЙиКЏЪ§ЮЊ
ЙигкЕуPЃЈ0ЃЌ1ЃЉЕФЯрЙиКЏЪ§ЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЕБnЃН0ЪБЃЌ
ЂйЖўДЮКЏЪ§yЃНx2ЙигкЕуPЕФЯрЙиКЏЪ§ЮЊЁЁ ЁЁЃЛ
ЂкЕуAЃЈ2ЃЌ3ЃЉдкЖўДЮКЏЪ§yЃНax2Љ2ax+aЃЈaЁй0ЃЉЙигкЕуPЕФЯрЙиКЏЪ§ЕФЭМЯѓЩЯЃЌЧѓaЕФжЕЃЛ
ЃЈ2ЃЉКЏЪ§![]() ЙигкЕуPЕФЯрЙиКЏЪ§ЪЧ
ЙигкЕуPЕФЯрЙиКЏЪ§ЪЧ![]() ЃЌдђnЃНЁЁ ЁЁЃЛ
ЃЌдђnЃНЁЁ ЁЁЃЛ
ЃЈ3ЃЉЕБ![]() nЉ1ЁмxЁм
nЉ1ЁмxЁм![]() n+3ЪБЃЌКЏЪ§
n+3ЪБЃЌКЏЪ§![]() ЕФЯрЙиКЏЪ§ЕФзюаЁжЕЮЊ7ЃЌЧѓnЕФжЕЃЎ
ЕФЯрЙиКЏЪ§ЕФзюаЁжЕЮЊ7ЃЌЧѓnЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂйyЃНЉx2ЃЛЂк![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЂйn=0ЪБЃЌЕуPЃЈ0ЃЌ0ЃЉЃЌдђЯрЙиКЏЪ§ЮЊЃКy=-x2ЃЌМДПЩЧѓНтЃЛ
ЂкЖўДЮКЏЪ§y=ax2-2ax+aЕФЖЅЕуЮЊЃКЃЈ1ЃЌ0ЃЉЃЌаТКЏЪ§ЕФЖЅЕуЮЊЃЈ-1ЃЌ0ЃЉЃЌдђаТКЏЪ§ЕФБэДяЪНЮЊЃКy=-aЃЈx+1ЃЉ2ЃЌНЋЕуAЕФзјБъДњШыЩЯЪНВЂНтЕУЃКa=-![]() ЃЛ
ЃЛ
ЃЈ2ЃЉСНИіКЏЪ§ЕФЖЅЕуЗжБ№ЮЊЃКЃЈ0ЃЌ![]() ЃЉЁЂЃЈ0ЃЌ-
ЃЉЁЂЃЈ0ЃЌ-![]() ЃЉЃЌгЩжаЕуЙЋЪНМДПЩЧѓНтЃЛ
ЃЉЃЌгЩжаЕуЙЋЪНМДПЩЧѓНтЃЛ
ЃЈ3ЃЉЗжnЁм-3ЁЂ-3ЃМnЁм1ЁЂnЃО1Ш§жжЧщПіЃЌЗжБ№ЧѓНтМДПЩЃЎ
НтЃКЃЈ1ЃЉЂйnЃН0ЪБЃЌЕуPЃЈ0ЃЌ0ЃЉЃЌдђЯрЙиКЏЪ§ЮЊЃКyЃНЉx2ЃЌ
ЙЪД№АИЮЊЃКyЃНЉx2ЃЛ
ЂкЖўДЮКЏЪ§yЃНax2Љ2ax+aЕФЖЅЕуЮЊЃКЃЈ1ЃЌ0ЃЉЃЌаТКЏЪ§ЕФЖЅЕуЮЊЃЈЉ1ЃЌ0ЃЉЃЌ
дђаТКЏЪ§ЕФБэДяЪНЮЊЃКyЃНЉaЃЈx+1ЃЉ2ЃЌ
НЋЕуAЕФзјБъДњШыЩЯЪНВЂНтЕУЃКaЃНЉ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉСНИіКЏЪ§ЕФЖЅЕуЗжБ№ЮЊЃКЃЈ0ЃЌ![]() ЃЉЁЂЃЈ0ЃЌЉ
ЃЉЁЂЃЈ0ЃЌЉ![]() ЃЉЃЌ
ЃЉЃЌ
гЩжаЕуЙЋЪНЕУЃК2nЃН![]() Љ
Љ![]() ЃЌНтЕУЃКnЃНЉ
ЃЌНтЕУЃКnЃНЉ![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊЃКЉ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉyЃНЉ2x2+nx![]() n2ЕФЖЅЕуЮЊЃКЃЈ
n2ЕФЖЅЕуЮЊЃКЃЈ![]() ЃЌЉn2ЃЉЃЌдђЯрЙиКЏЪ§ЖЅЕуЮЊЃКЃЈЉ
ЃЌЉn2ЃЉЃЌдђЯрЙиКЏЪ§ЖЅЕуЮЊЃКЃЈЉ![]() ЃЌn2+2nЃЉЃЌ
ЃЌn2+2nЃЉЃЌ
дђЯрЙиКЏЪ§ЕФБэДяЪНЮЊЃКyЃН2ЃЈx+![]() ЃЉ2+n2+2nЃЛ
ЃЉ2+n2+2nЃЛ
ЂйЕБnЁмЉ3ЪБЃЌ
КЏЪ§дкxЃН![]() n+3ЪБЃЌШЁЕУзюаЁжЕЃЌМД2ЃЈ
n+3ЪБЃЌШЁЕУзюаЁжЕЃЌМД2ЃЈ![]() +3+
+3+![]() ЃЉ2+n2+2nЃН7ЃЌ
ЃЉ2+n2+2nЃН7ЃЌ
НтЕУЃКnЃНЉ![]() ЛђЉ1ЃЈЩсШЅЉ1ЃЉЃЌ
ЛђЉ1ЃЈЩсШЅЉ1ЃЉЃЌ
ЙЪnЃНЉ![]() ЃЛ
ЃЛ
ЂкЕБЉ3ЃМnЁм1ЪБЃЌ
КЏЪ§дкЖЅЕуДІШЁЕУзюаЁжЕЃЌМДn2+2nЃН7ЃЌ
НтЕУЃКnЃНЉ1![]() ЃЈЩсШЅЃЉЃЛ
ЃЈЩсШЅЃЉЃЛ
ЂлЕБnЃО1ЪБЃЌ
ЭЌРэПЩЕУЃКnЃН![]() ЛђЉ1ЃЈЩсШЅЉ1ЃЉЃЌ
ЛђЉ1ЃЈЩсШЅЉ1ЃЉЃЌ
злЩЯЃЌnЃНЉ![]() Лђ
Лђ![]() ЃЎ
ЃЎ