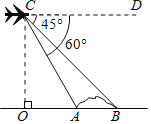
��Ŀ����
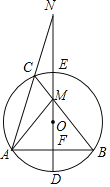
����Ŀ����ͼ1����֪������y��x2+bx��3��b�dz�������x�ύ��A��B���㣬��y�ύ�ڵ�C���ҵ�A����Ϊ����1��0����
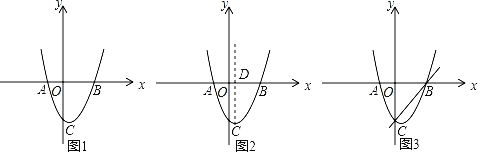
��1����Ò����ߵĽ���ʽ�ͶԳ��
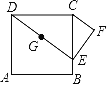
��2����ͼ2�������ߵĶԳ�����x�ύ�ڵ�D���ڶԳ�������һ����E��ʹ��OAC����ODE���ƣ�ֱ��д����E�����ꣻ
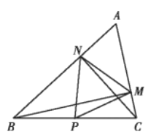
��3����ͼ3��ƽ����x���ֱ���������߽���P��x1��y1����Q��x2��y2�����㣬��ֱ��BC���ڵ�N��x3��y3������x1��x2��x3ʱ�����ͼ����x1+x2+x3��ȡֵ��Χ��
���𰸡���1��y��x2��2x��3��x��1����2����E��1����3����1��3����1��![]() ����1����
����1����![]() ������3��x1+x2+x3��5
������3��x1+x2+x3��5
��������
��1���ɴ���ϵ�����������ʽ���ɵöԳ��
��2��������������ۣ������������ε����ʿɵ���⣻
��3���ɶ��κ��������ʿɵ�x1+x2=2��������ɵ�x3��3��������⣮
��1����������y��x2+bx��3��b�dz�������x�ύ��A��B���㣬
��0��1��b��3
��b����2��
�������߽���ʽΪ��y��x2��2x��3��
��y��0ʱ��x1����1��x2��3��
��B��3��0��
��Գ���Ϊֱ��x��1��
��2����������y��x2��2x��3��y�ύ�ڵ�C��
���C��0����3�����ҵ�A����Ϊ����1��0����
��OA��1��OB��3��
�ߡ�OAC����ODE���ƣ��ҡ�AOC����ODE��90����
��![]() ��
��![]() ��
��
��DE��3��![]() ��
��
���E��1����3����1��3����1��![]() ����1����
����1����![]() ����
����
��3���ߵ�B��3��0������C��0����3��
��ֱ��BC�Ľ���ʽΪ��y��x��3��
��ƽ����x���ֱ���������߽���P��x1��y1����Q��x2��y2�����㣬
���P����Q���ڶԳ���Գƣ�
��x1+x2��2��
��x1��x2��x3��
��ֱ��PQ��AB���Ϸ���
��x3��3��
��x1+x2+x3��5��

����Ŀ��ij�̵���ÿ��50Ԫ�ļ۸�800��![]() ������һ�����Ե���80Ԫ���ۣ��۳���200�����ڶ�����������۲��䣬Ԥ���Կ��۳�200�������̵�Ϊ���������������������ۣ������г����飬����ÿ����1Ԫ���ɶ����۳�10��������͵���Ӧ������50Ԫ���ڶ����½������̵��ʣ���T��һ������֣����ʱ����Ϊ40Ԫ����ڶ����µ��۽���
������һ�����Ե���80Ԫ���ۣ��۳���200�����ڶ�����������۲��䣬Ԥ���Կ��۳�200�������̵�Ϊ���������������������ۣ������г����飬����ÿ����1Ԫ���ɶ����۳�10��������͵���Ӧ������50Ԫ���ڶ����½������̵��ʣ���T��һ������֣����ʱ����Ϊ40Ԫ����ڶ����µ��۽���![]() Ԫ��
Ԫ��
��1��������ú�![]() �Ĵ���ʽ��ɱ����еĢ٢ڢ۴���
�Ĵ���ʽ��ɱ����еĢ٢ڢ۴���
ʱ�� | ��һ���� | �ڶ����� | ��� |
���ۣ�Ԫ�� | 80 | _______ | 40 |
������������ | 200 | _______ | _______ |
��2��������̵�ϣ��ͨ��������800��![]() ������9000Ԫ����ô�ڶ����µ��۽��Ͷ���Ԫ��
������9000Ԫ����ô�ڶ����µ��۽��Ͷ���Ԫ��