题目内容
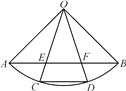
【题目】如图,四边形![]() 内接于
内接于![]() ,点
,点![]() 在对角线
在对角线![]() 上,
上,![]() .
.
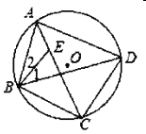
(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)求证:![]() .
.
【答案】(1)![]() ; (2)见解析
; (2)见解析
【解析】
(1)根据等腰三角形的性质由BC=DC得到∠CBD=∠CDB=40°,再根据圆周角定理得∠BAC=∠CDB=40°,∠CAD=∠CBD=40°,所以∠BAD=∠BAC+∠CAD=80°;
(2)根据等腰三角形的性质由EC=BC得∠CEB=∠CBE,再利用三角形外角性质得∠CEB=∠2+∠BAE,则∠2+∠BAE=∠1+∠CBD,加上∠BAE=∠CBD,所以∠1=∠2.
(1)解:∵BC=DC,
∴∠CBD=∠CDB=40°,
∵∠BAC=∠CDB=40°,∠CAD=∠CBD=40°,
∴∠BAD=∠BAC+∠CAD=40°+40°=80°;
(2)证明:∵EC=BC,
∴∠CEB=∠CBE,
而∠CEB=∠2+∠BAE,∠CBE=∠1+∠CBD,
∴∠2+∠BAE=∠1+∠CBD,
∵∠BAE=∠BDC=∠CBD,
∴∠1=∠2.

练习册系列答案
 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
【题目】某商店以每件50元的价格购进800件![]() 恤,第一个月以单价80元销售,售出了200件.第二个月如果单价不变,预计仍可售出200件,该商店为增加销售量决定降价销售,根据市场调查,单价每降低1元,可多销售出10件,但最低单价应不低于50元,第二个月结束后,该商店对剩余的T恤一次性清仓,清仓时单价为40元.设第二个月单价降低
恤,第一个月以单价80元销售,售出了200件.第二个月如果单价不变,预计仍可售出200件,该商店为增加销售量决定降价销售,根据市场调查,单价每降低1元,可多销售出10件,但最低单价应不低于50元,第二个月结束后,该商店对剩余的T恤一次性清仓,清仓时单价为40元.设第二个月单价降低![]() 元,
元,
(1)填表(用含![]() 的代数式完成表格中的①②③处)
的代数式完成表格中的①②③处)
时间 | 第一个月 | 第二个月 | 清仓 |
单价(元) | 80 | _______ | 40 |
销售量(件) | 200 | _______ | _______ |
(2)如果该商店希望通过销售这800件![]() 恤获利9000元,那么第二个月单价降低多少元?
恤获利9000元,那么第二个月单价降低多少元?