题目内容
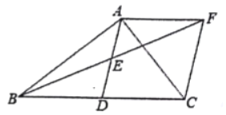
【题目】如图,在![]() 中,
中,![]() ,AD是BC边上的中线,点E为AD的中点,过点A作
,AD是BC边上的中线,点E为AD的中点,过点A作![]() 交BE的延长线于点F,连接CF.
交BE的延长线于点F,连接CF.
(1)求证:![]() ;
;
(2)连接DF,当![]() 度时,四边形ABDF为菱形?证明你的结论.
度时,四边形ABDF为菱形?证明你的结论.
【答案】(1)见解析;(2)30
【解析】
(1)根据直角三角形的性质得到AD=CD=BD,然后证明△AEF≌△DEB即可得到结论;
(2)由条件可知四边形ABDF是平行四边形,然后通过30°所对的直角边为斜边的一半,得到AB=BD,于是得到结论.
(1)证明:∵∠BAC=90°,AD是BC边上的中线,
∵AD=CD=BD=![]() BC,
BC,
∵点E为AD的中点,
∴AE=DE,
∵AF∥BC,
∴∠AFE=∠DBE,
∵∠AEF=∠DEB,
∴△AEF≌△DEB(AAS),
∴AF=BD,
∴AD=AF;
(2)30°;
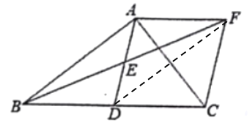
由(1)可知AF=BD,
∵AF∥BC,
∴四边形ABDF是平行四边形,
∵∠BAC=90°,∠ACB=30°,
∴AB=![]() BC =BD,
BC =BD,
∴平行四边形ABDF为菱形.

 阅读快车系列答案
阅读快车系列答案【题目】今年疫情防控期间,我市一家服装有限公司生产了一款服装,为对比分析以前实体商店和现在网上商店两种途径的销售情况,进行了为期30天的跟踪调查.其中实体商店的日销售量![]() (百件)与时间
(百件)与时间![]() (
(![]() 为整数,单位:天)的部分对应值如下表所示;网上商店的日销售量
为整数,单位:天)的部分对应值如下表所示;网上商店的日销售量![]() (百件)与时间
(百件)与时间![]() (
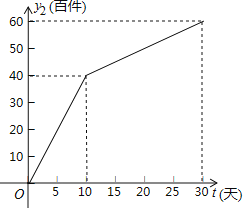
(![]() 为整数,单位:天)的关系如图所示.
为整数,单位:天)的关系如图所示.
时间 | 0 | 6 | 10 | 12 | 18 | 20 | 24 | 30 |
日销售量 | 0 | 72 | 100 | 108 | 108 | 100 | 72 | 0 |
(1)请你在一次函数、二次函数和反比例函数中,选择合适的函数反映![]() 与
与![]() 的变化规律,并求出
的变化规律,并求出![]() 与
与![]() 的函数关系式及自变量
的函数关系式及自变量![]() 的取值范围;
的取值范围;
(2)求![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)在跟踪调查的30天中,设实体商店和网上商店的日销售总量为![]() (百件),求
(百件),求![]() 与
与![]() 的函数关系式;当
的函数关系式;当![]() 为何值时,日销售量
为何值时,日销售量![]() 达到最大,并求出此时的最大值.
达到最大,并求出此时的最大值.