题目内容
【题目】如图①,在矩形ABCD中,AB<AD,对角线AC,BD相交于点O,动点P由点A出发,沿AB-BC→CD向点D运动设点P的运动路程为x,△AOP的面积为y,y与x的函数关系图象如图②所小示,则AD的长为________.

【答案】4
【解析】
当P点在AB上运动时,△AOP面积逐渐增大,当P点到达B点时,结合图象可得△AOP面积最大为3,得到AB与BC的积为12;当P点在BC上运动时,△AOP面积逐渐减小,当P点到达C点时,△AOP面积为0,此时结合图象可知P点运动路径长为7,得到AB与BC的和为7,构造关于AB的一元二方程可求解.
①当点P在AB上运动时,y=![]() AP·×
AP·×![]() AD
AD
由图象可知:△AOP面积逐渐增大,当P点到达B点时,△AOP面积最大为3,此时 y=![]() AB×
AB×![]() BC=
BC=![]() AB·BC=3,即AB·BC=12;
AB·BC=3,即AB·BC=12;
②当P点在BC上运动时,△AOP面积逐渐减小,当P点到达C点时,由图象可知,此时△AOP面积的为0,P点运动路径长为7,即AB+BC=7
∴BC=7-AB,代入ABBC=12,得:
AB(7-AB)=12,解得AB=4或3
又∵AB<AD,即AB<BC
∴AB=3,BC=4.
∴AD=4
故答案为:4

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案【题目】为了加强对校内外安全监控,创建平安校园,某学校计划增加15台监控摄像设备,现有甲、乙两种型号的设备,其中每台价格,有效监控半径如表所示,经调查,购买1台甲型设备比购买1台乙型设备多150元,购买2台甲型设备比购买3台乙型设备少400元.
甲型 | 乙型 | |
价格(元/台) | a | b |
有效半径(米/台) | 150 | 100 |
(1)求a、b的值;
(2)若购买该批设备的资金不超过11000元,且要求监控半径覆盖范围不低于1600米,两种型号的设备均要至少买一台,请你为学校设计购买方案,并计算最低购买费用.
【题目】10月21日,“中国流动科技馆”巡展启动仪式在新华区青少年活动中心盛大举行,此次巡展以“体验科学”为主题.该区某中学举行了“科普知识”竞赛,为了解此次“科普知识”竞赛成绩的情况,随机抽取了部分参赛学生的成绩,整理并制作出如下的不完整的统计表和统计图,如图所示.请根据图表信息解答以下问题.
组别 | 成绩 | 频数 |
A组 |
|
|
B组 |
| 12 |
C组 |
| 18 |
D组 |
| 21 |
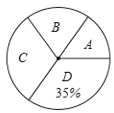
(1)表中一共抽取了________个参赛学生的成绩;![]() ________;
________;
(2)求出计算扇形统计图中“![]() ”的圆心角度数.
”的圆心角度数.
(3)若成绩在90分以上(包括90分)的为“优”等,已知该校共有1200名学生,请你估计该校约有多少名学生的成绩是“优”等.