题目内容
【题目】某茶具店购进了A、B两种不同的茶具,1套A种茶具和2套B种茶具共需250元;3套A种茶具和4套B种茶具共需600元.
(1)求A、B两种茶具每套的进价分别是多少元?
(2)由于茶具畅销,茶具店准备再购进A、B两种茶具共80套,但这次进货时,工厂对A种茶具每套进价提高了8%,而B种茶具每套按第一次进价的八折,若茶具店本次进货总钱数不超过6240元,则最多可进A种茶具几套?
(3)若销售一套A种茶具可获利30元,销售一套B种茶其可获利20元,在(2)的条件下,如何进货可使本次购进茶具获利最多?最多是多少?
【答案】(1)A、B 两种茶具每套的进价分别是100元和75元
(2)30套
(3)进30套A种茶具,50套B种茶具;获利最多为1900元
【解析】
(1)根据题意,列出二元一次方程组,从而可以得到A、B两种茶具每套的进价分别是多少元;
(2)根据题意,可以得到相应的不等式,从而可以得到购买A种茶具数量的取值范围,然后即可得到最多可进A种茶具几套;
(3)根据题意,可以得到利润与购买A种数量的函数关系,然后根据一次函数的性质,即可得到如何进货可使本次购进茶具获利最多,最多是多少.
(1)设 A、B 两种茶具每套的进价分别是x元、y元,根据题意,可得
![]()
解得![]()
答:A、B 两种茶具每套的进价分别是100元和75元.
(2)设购进A种茶具a套,根据题意,可得
![]() .
.
解得![]() .
.
答:最多可进 A 种茶具30套.
(3)设获利为w元,则
![]() .
.
∵![]() ,所以w随的增大而增大.
,所以w随的增大而增大.
∵![]() ,∴当
,∴当 ![]() 时,
时, ![]() (元)
(元)
此时,![]() ,
,
答:进30套A种茶具,50套B种茶具,可使本次购进茶具获利最多,获利最多为1900元.

 阅读快车系列答案
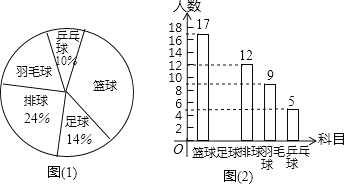
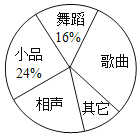
阅读快车系列答案【题目】某校为了庆祝建国七十周年,决定举办一台文艺晚会,为了了解学生最喜爱的节目形式,随机抽取了部分学生进行调查,规定每人从“歌曲”,“舞蹈”,“小品”,“相声”和“其它”五个选项中选择一个,并将调查结果绘制成如下两幅不完整的统计图表,请根据图中信息,解答下列题:
最喜爱的节目 | 人数 |
歌曲 | 15 |
舞蹈 | a |
小品 | 12 |
相声 | 10 |
其它 | b |
(1)在此次调查中,该校一共调查了 名学生;
(2)a= ;b= ;
(3)在扇形计图中,计算“歌曲”所在扇形的圆心角的度数;
(4)若该校共有1200名学生,请你估计最喜爱“相声”的学生的人数.
【题目】我市某初中课外兴趣活动小组对某水稻品种的稻穗谷粒数目进行调查,从试验田中随机抽取了30株,得到的数据如下(单位:颗):
182 | 195 | 201 | 179 | 208 | 204 | 186 | 192 | 210 | 204 |
175 | 193 | 200 | 203 | 188 | 197 | 212 | 207 | 185 | 206 |
188 | 186 | 198 | 202 | 221 | 199 | 219 | 208 | 187 | 224 |
(1)对抽取的30株水稻稻穗谷粒数进行统计分析,请补全下表中空格,并完善直方图:
谷粒颗数 | 175≤x<185 | 185≤x<195 | 195≤x<205 | 205≤x<215 | 215≤x<225 |
频数 | 8 | 10 | 3 | ||
对应扇形 图中区域 | D | E | C |

(2)如图所示的扇形统计图中,扇形A对应的圆心角为 度,扇形B对应的圆心角为 度;
(3)该试验田中大约有3000株水稻,据此估计,其中稻穗谷粒数大于或等于205颗的水稻有多少株?