题目内容
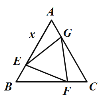
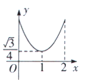
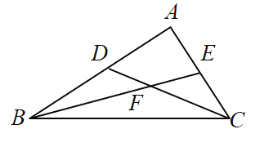
【题目】如图,已知![]() 的顶点
的顶点![]() ,
,![]() ,点
,点![]() 在
在![]() 轴的正半轴上,
轴的正半轴上,![]() 在
在![]() 轴的正半轴上.连接
轴的正半轴上.连接![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,
,![]() 交
交![]() 于点
于点![]() ,则点
,则点![]() 的坐标为( )
的坐标为( )
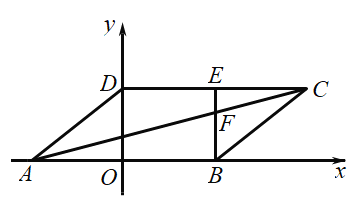
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】D
【解析】
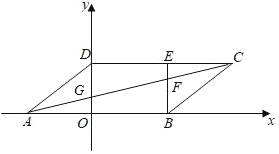
设AC与OD交于点G,由平行四边形的性质得出AB∥CD,AB=CD,则CD⊥OD,由题意的OA=4,AB=CD=8,OD=3,则OB=AB-OA=4,证△OAG∽△DCG,求出OG=![]() DG=
DG=![]() OD=1,证
OD=1,证![]() ,求出BF=2,即可得出答案.
,求出BF=2,即可得出答案.
解:设AC与OD交于点G,如图所示:
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∵AB⊥OD,
∴CD⊥OD,
∵A(-4,0),C(8,3),
∴OA=4,AB=CD=8,OD=3,
∴OB=AB-OA=4,
∵AB∥CD,
∴![]() ,
,
∴ ![]()
∴OG=![]() DG=
DG=![]() OD=1,
OD=1,
∵BE⊥CD,CD⊥OD,
∴OD∥BE, ∴![]() ,
,
∴ ![]() ,即
,即![]()
解得:BF=2,
∴点F的坐标为(4,2),
故选![]()

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目