题目内容
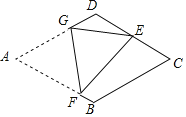
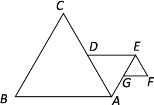
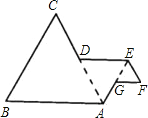
【题目】如图，作等边△ABC，取AC的中点D，以AD为边向△ABC形外作等边△ADE，取AE的中点G，再以EG为边作等边△EFG，如此反复，当作出第6个三角形时，若AB=4，整个图形的外围周长是______.
【答案】
【解析】
利用平移性质可得图形ABCDEFG外围的周长等于等边三角形△ABC的周长加上AE，GF长，同理可得整个图形的外围周长等于等边三角形△ABC的周长加上后面所作的各等边三角形的边长．
解：∵△ABC、△ADE与△EFG都是等边三角形
∴AD=DE，EF=EG
∵D和G分别为AC和AE的中点，AB=4
∴DE=EA=AD=2，GF=EF=GE=1，
∴图形ABCDEFG外围的周长=△ABC的周长+AE+GF．
同理，当作出第6个三角形时，整个图形的外围周长是：
△ABC的周长+2+1+
+
+
=4
=15+
= .
故答案为： .
练习册系列答案
阅读快车系列答案
相关题目
