题目内容
【题目】如图,在△ABC中,∠ACB=100°,AC=AE,BC=BD,则∠DCE的度数为
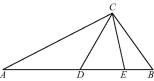
A. 20° B. 25° C. 30° D. 40°
【答案】D
【解析】
根据此题的条件，找出等腰三角形，找出相等的边与角度，设出未知量，找出满足条件的方程．
解：∵AC=AE，BC=BD
∴设∠AEC=∠ACE=x°，∠BDC=∠BCD=y°，
∴∠A=180°-2x°，
∠B=180°-2y°，
∵∠ACB+∠A+∠B=180°，
∴100+（180-2x）+（180-2y）=180，得x+y=140，
∴∠DCE=180-（∠AEC+∠BDC）=180-（x+y）=40°．故选D．
根据题目中的等边关系，找出角的相等关系，再根据三角形内角和180°的定理，列出方程，解决此题．
练习册系列答案
轻松暑假总复习系列答案
相关题目
【题目】为庆祝元旦，某校组织大合唱汇演．初一(1)、(2)班学生准备统一购买服装参加演出（一人买一套），这两班共有学生104名学生参加演出，其中(1)班人数较少，不足50人．下面是某服装厂给出的服装价格表：
购买服装的套数 | 1﹣50套 | 51﹣100套 | 100套以上 |
每套服装的价格 | 130元 | 110元 | 90元 |
经估算，如果两个班都以班为单位购买服装，那么一共应付12400元，问：
(1)两班各有多少学生？
(2)如果两班联合起来，作为一个团体购买服装，可省多少钱？
(3)如果(2)班不购买了，只有(1)班单独购买，作为组织者的你将如何购买才最省钱？