题目内容
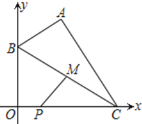
【题目】如图,一次函数y=k1x+b的图象与反比例函数y=![]() (x<0)的图象相交于点A(-1,2)、点B(-4,n).
(x<0)的图象相交于点A(-1,2)、点B(-4,n).
(1)求此一次函数和反比例函数的表达式;
(2)求△AOB的面积;
(3)在x轴上存在一点P,使△PAB的周长最小,求点P的坐标.
【答案】(1) ![]() ;(2)
;(2) ![]() ;(3)P点坐标为(
;(3)P点坐标为(![]() ,0)
,0)
【解析】分析:(1)由点A的坐标求反比例函数的解析式,得到点B的坐标,待定系数法求一次函数的解析式;(2)分别过点A,B用坐标轴的平行线构造矩形,用图形面积的和差关系求三角形AOB的面积;(3)作点A关于x轴的对称点A′,直线A′B与x轴的交点即是点P.
详解:(1)∵反比例![]() 的图象经过点A(—1,2),
的图象经过点A(—1,2),
∴![]() =—1×2=—2,
=—1×2=—2,
∴反比例函数表达式为:![]() ,
,
∵反比例![]() 的图象经过点B(—4,n),
的图象经过点B(—4,n),
∴—4n=—2,![]() ,∴B点坐标为(—4,
,∴B点坐标为(—4,![]() ),
),
∵直线![]() 经过点A(—1,2),点B(—4,
经过点A(—1,2),点B(—4,![]() ),
),
∴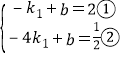 ,
,
①—②,得:3![]() ,∴
,∴![]() ,
,
把![]() 代入①,得:b=
代入①,得:b=![]() ,
,
∴一次函数表达式为:![]() .
.
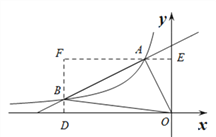
(2)如图1所示,分别过点B作BD⊥x轴,垂足为D,过点A作AE⊥y轴,垂足为E,则四边形ODFE为矩形,
∵点A(—1,2),点B(—4,![]() ),
),
∴OD=EF=4,OE=DF=2,AE=1,BD=![]() ,
,
∴![]() ,
,![]() .
.
∵点A,点B在函数![]() 的图象上,∴
的图象上,∴![]()
∴![]() .
.
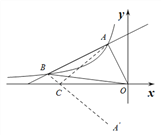
(3)如图2所示,作点A关于x轴的对称点A′,连接A′B,交x轴于点P,此时△PAB的周长最小,
∵点A′和A(—1,2)关于x轴对称,∴点A′的坐标为(—1,—2),
设直线A′B的表达式为![]()
∵经过点A′(—1,—2),点B(—4,![]() ),∴
),∴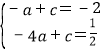
解得:![]() ,
,![]() .
.
∴直线A′B的表达式为:![]() .
.
当y=0时,则x=![]() ,∴P点坐标为(
,∴P点坐标为(![]() ,0).
,0).

练习册系列答案
相关题目