题目内容
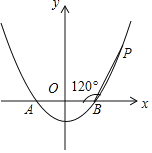
【题目】如图,已知抛物线![]() 与x轴相交于A,B两点,点P是抛物线上一点,且
与x轴相交于A,B两点,点P是抛物线上一点,且![]() ,
,![]() .
.
![]() 求该抛物线的表达式;
求该抛物线的表达式;
![]() 设点
设点![]() 为抛物线上的一个动点,当点M在曲线BA之间
为抛物线上的一个动点,当点M在曲线BA之间![]() 含端点
含端点![]() 移动时,求
移动时,求![]() 的最大值及取得最大值时点M的坐标.
的最大值及取得最大值时点M的坐标.
【答案】(1)抛物线解析式为;y=![]() x2﹣
x2﹣![]() ;(2)当点M在曲线BA之间(含端点)移动时,M的坐标为(
;(2)当点M在曲线BA之间(含端点)移动时,M的坐标为(![]() ,﹣
,﹣![]() )或(﹣
)或(﹣![]() ,﹣
,﹣![]() )时,|m|+|n|的最大值为
)时,|m|+|n|的最大值为![]() .
.
【解析】
(1)先求出A、B两点坐标,然后过点P作PC⊥x轴于点C,根据∠PBA=120°,PB=AB,分别求出BC和PC的长度即可得出点P的坐标,最后将点P的坐标代入二次函数解析式即;
(2)根据题意可知:n<0,然后对m的值进行分类讨论,当﹣2≤m≤0时,|m|=﹣m;当0<m≤2时,|m|=m,列出函数关系式即可求得|m|+|n|的最大值.
(1)如图,令y=0代入y=ax2﹣4a,
∴0=ax2﹣4a,
∵a>0,
∴x2﹣4=0,
∴x=±2,
∴A(﹣2,0),B(2,0),
∴AB=4,
过点P作PC⊥x轴于点C,
∴∠PBC=180°﹣∠PBA=60°,
∵PB=AB=4,
∴cos∠PBC=![]() ,
,
∴BC=2,
由勾股定理可求得:PC=2![]() ,
,
∵OC=OB+BC=4,
∴P(4,2![]() ),
),
把P(4,2![]() )代入y=ax2﹣4a,
)代入y=ax2﹣4a,
∴2![]() =16a﹣4a,
=16a﹣4a,
∴a=![]() ,
,
∴抛物线解析式为:y=![]() x2﹣
x2﹣![]() ;
;
(2)当点M在曲线BA之间(含端点)移动时,
∴﹣2≤m≤2,n<0,
当﹣2≤m≤0时,
∴|m|+|n|=﹣m﹣n=﹣![]() m2﹣m+
m2﹣m+![]() =﹣
=﹣![]() (m+
(m+![]() )2+
)2+![]() ,
,
当m=﹣![]() 时,
时,
∴|m|+|n|可取得最大值,最大值为![]() ,
,
此时,M的坐标为(﹣![]() ,﹣
,﹣![]() ),
),
当0<m≤2时,
∴|m|+|n|=m﹣n=﹣![]() m2+m+
m2+m+![]() =﹣
=﹣![]() (m﹣
(m﹣![]() )2+
)2+![]() ,
,
当m=![]() 时,
时,
∴|m|+|n|可取得最大值,最大值为![]() ,
,
此时,M的坐标为(![]() ,﹣
,﹣![]() ),
),
综上所述,当点M在曲线BA之间(含端点)移动时,M的坐标为(![]() ,﹣
,﹣![]() )或(﹣
)或(﹣![]() ,﹣
,﹣![]() )时,|m|+|n|的最大值为
)时,|m|+|n|的最大值为![]() .
.


 黄冈创优卷系列答案
黄冈创优卷系列答案