题目内容
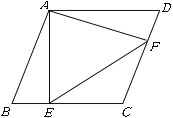
【题目】如图,在菱形ABCD中,∠B=60°,点E、F分别从点B、D出发以同样的速度沿边BC、DC向点![]() 运动.给出以下四个结论:①AE=AF②∠CEF=∠CFE③当点E、F分别为边BC、DC的中点时,△AEF是等边三角形④当点E、F分别为边BC、DC的中点时,△AEF的面积最大.上述结论中正确的序号有________.(把你认为正确的序号都填上)
运动.给出以下四个结论:①AE=AF②∠CEF=∠CFE③当点E、F分别为边BC、DC的中点时,△AEF是等边三角形④当点E、F分别为边BC、DC的中点时,△AEF的面积最大.上述结论中正确的序号有________.(把你认为正确的序号都填上)
【答案】①③④
【解析】
试题根据菱形的性质对各个结论进行验证从而得到正确的序号.
解:∵点E、F分别从点B、D出发以同样的速度沿边BC、DC向点C运动,
∴BE=DF,
∵AB=AD,∠B=∠D,
∴△ABE≌△ADF,
∴AE=AF,①正确;
∴CE=CF,
∴∠CEF=∠CFE,②正确;
∵在菱形ABCD中,∠B=60°,
∴AB=BC,
∴△ABC是等边三角形,
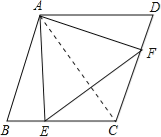
∴当点E,F分别为边BC,DC的中点时,BE=AB,DF=AD,
∴△ABE和△ADF是直角三角形,且∠BAE=∠DAF=30°,
∴∠EAF=120°﹣30°﹣30°=60°,
∴△AEF是等边三角形,③正确;
∵△AEF的面积=菱形ABCD的面积﹣△ABE的面积﹣△ADF的面积﹣△CEF的面积=![]() AB2﹣BEAB×
AB2﹣BEAB×![]() ×2﹣×
×2﹣×![]() ×(AB﹣BE)2=﹣
×(AB﹣BE)2=﹣![]() BE2+
BE2+![]() AB2,
AB2,
∴△AEF的面积是BE的二次函数,
∴当BE=0时,△AEF的面积最大,④错误.
故正确的序号有①②③.

练习册系列答案
相关题目