题目内容

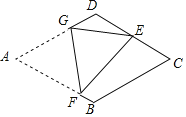
【题目】如图，在菱形纸片ABCD中，AB＝4，∠A＝60°，将菱形纸片翻折，使点A落在CD的中点E处，折痕为FG，点F、G分别在边AB、AD上．则sin∠EFG的值为________．

【答案】

【解析】试题解析：作EH⊥AD于H，连接BE、BD，连接AE交FG于O，如图，

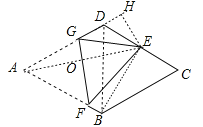
∵四边形ABCD为菱形，∠A=60°，∴△BDC为等边三角形，∠ADC=120°，∵E点为CD的中点，∴CE=DE=1，BE⊥CD，在Rt△BCE中，BE= CE=，∵AB∥CD，∴BE⊥AB，设AF=x，∵菱形纸片翻折，使点A落在CD的中点E处，折痕为FG，点F，G分别在边AB，AD上，∴EF=AF，FG垂直平分AE，∠EFG=∠AFG，在Rt△BEF中，（2﹣x）2+（）2=x2，解得x=，在Rt△DEH中，DH=DE=，HE=DH=，在Rt△AEH中，AE=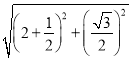 =，∴AO=，在Rt△AOF中，OF=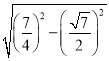 =，∴cos∠AFO= =．故答案为： ．

练习册系列答案
相关题目

【题目】阅读材料：

小明在学习了二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如3＋2 ＝(1＋)2.善于思考的小明进行了以下探索：

设a＋b＝(m＋n)2(其中a，b，m，n均为正整数)，则有a＋b＝m2＋2n2＋2mn.

∴a＝m2＋2n2，b＝2mn.这样小明就找到了一种把部分形如a＋b的式子化为平方式的方法．

请你仿照小明的方法探索并解决下列问题：

(1)当a，b，m，n均为正整数时，若a＋b＝(m＋n)2，用含m，n的式子分别表示a，b，得a＝__________，b＝__________；

(2)利用所探索的结论，找一组正整数a，b，m，n填空：________＋________＝(________＋________)2；

(3)若a＋4＝(m＋n)2，且a，m，n均为正整数，求a的值．

【题目】如图，已知⊙O分别切△ABC的三条边AB、BC、CA于点D、E、F，S△ABC=10cm2，C△ABC=10cm且∠C=60°．求：

（1）⊙O的半径r；

（2）扇形OEF的面积（结果保留π）；

（3）扇形OEF的周长（结果保留π）

【题目】如图，在正方形ABCD中，P是对角线AC上的一点，点E在BC的延长线上，且PE=PB．

（1）当PC=CE时，求∠CDP的度数；

（2）试用等式表示线段PB、BC、CE之间的数量关系，并证明．

【题目】下列函数中，自变量的取值范围选取错误的是

A.y=2x2中，x取全体实数

B.y=中，x取x≠-1的实数

C.y=中，x取x≥2的实数

D.y=中，x取x≥-3的实数

【题目】如图，甲转盘被分成3个面积相等的扇形，乙转盘被分成4个面积相等的扇形，每一个扇形都标有相应的数字．同时转动两个转盘，当转盘停止后，设甲转盘中指针所指区域内的数字为x，乙转盘中指针所指区域内的数字为y（当指针指在边界线上时，重转一次，直到指针指向一个区域为止）．

（1）请你用画树状图或列表格的方法，列出所有等可能情况，并求出点（x，y）落在坐标轴上的概率；

（2）直接写出点（x，y）落在以坐标原点为圆心，2为半径的圆内的概率为_________．

【题目】如图，抛物线y＝ax 2＋bx＋c的顶点为M（1，4），与x轴的右交点为A，与y轴的交点为B，点C与点B关于抛物线的对称轴对称，且S△ABC ＝3．

（1）求抛物线的解析式；

（2）点D是y轴上一点，将点D绕C点逆时针旋转90°得到点E，若点E恰好落在抛物线上，请直接写出点D的坐标；

（3）设抛物线的对称轴与直线AB交于点F，问：在x轴上是否存在点P，使得以P、A、F为顶点的三角形与△ABC相似？若存在，求点P的坐标；若不存在，请说明理由

【题目】1955年，印度数学家卡普耶卡（）研究了对四位自然数的一种变换：任给出四位数，用的四个数字由大到小重新排列成一个四位数，再减去它的反序数（即将的四个数字由小到大排列，规定反序后若左边数字有0，则将0去掉运算，比如0001，计算时按1计算），得出数，然后继续对重复上述变换，得数，…，如此进行下去，卡普耶卡发现，无论是多大的四位数，只要四个数字不全相同，最多进行次上述变换，就会出现变换前后相同的四位数，这个数称为变换的核.则四位数9631的变换的核为______.

【题目】如图,在△ABC中,点E在AC上,∠AEB=∠ABC.

(1)图1中,作∠BAC的角平分线AD,分别交CB、BE于D、F两点,求证:∠EFD=∠ADC；

(2)图2中,作△ABC的外角∠BAG的角平分线AD,分别交CB、BE的延长线于D、F两点,试探究(1)中结论是否仍成立?为什么?

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网