题目内容
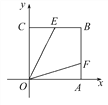
【题目】将一矩形纸片OABC放在平面直角坐标系中,O为原点,点A在x轴上,点C在y轴上,OA=10,OC=8,如图在OC边上取一点D,将△BCD沿BD折叠,使点C恰好落在OA边上,记作E点;
(1)求点E的坐标及折痕DB的长;
(2)在x轴上取两点M、N(点M在点N的左侧),且MN=4.5,求使四边形BDMN的周长最短的点M、点N的坐标。
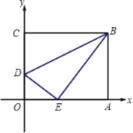
【答案】(1)E(4,0);DB=5![]() ;(2)M(1.5,0);N(6,0);
;(2)M(1.5,0);N(6,0);
【解析】
(1)、根据矩形的性质得到BC=OA=10,AB=OC=8,再根据折叠的性质得到BC=BE=10,DC=DE,易得AE=6,则OE=10-6=4,即可得到E点坐标;在Rt△ODE中,设DE=x,则OD=OC-DC=OC-DE=8-x,利用勾股定理可计算出x,再在Rt△BDE中,利用勾股定理计算出BD;(2)、以D、M、N为顶点作平行四边形DMND′,作出点B关于x轴对称点B′,则易得到B′的坐标,D′的坐标,然后利用待定系数法求出直线D′B′的解析式,令y=0,得-2x+12=0,确定N点坐标,也即可得到M点坐标.
(1)、∵四边形OABC为矩形, ∴BC=OA=10,AB=OC=8,
∵△BCD沿BD折叠,使点C恰好落在OA边E点上, ∴BC=BE=10,DC=DE,
在Rt△ABE中,BE=10,AB=8, ∴AE=6, ∴OE=10-6=4, ∴E点坐标为(4,0);
在Rt△ODE中,设DE=x,则OD=OC-DC=OC-DE=8-x, ∴x2=42+(8-x)2,解得x=5,
在Rt△BDE中, BD=![]() ;
;
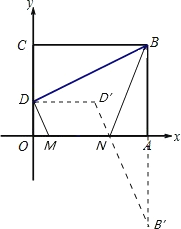
(2)、以D、M、N为顶点作平行四边形DMND′,作出点B关于x轴对称点B′,如图,
∴B′的坐标为(10,-8),DD′=MN=4.5,∴D′的坐标为(4.5,3),
设直线D′B′的解析式为y=kx+b,
把B′(10,-8),D′(4.5,3)代入得,10k+b=-8,4.5k+b=3,解得k=-2,b=12,
∴直线D′B′的解析式为y=-2x+12, 令y=0,得-2x+12=0,解得x=6,
∴M(1.5,0);N(6,0).

【题目】随着人民生活水平的提高,购买老年代步车的人越来越多.这些老年代步车却成为交通安全的一大隐患.针对这种现象,某校数学兴趣小组在《老年代步车现象的调查报告》中就“你认为对老年代步车最有效的管理措施”随机对某社区部分居民进行了问卷调查,其中调查问卷设置以下选项(只选一项):
A:加强交通法规学习;
B:实行牌照管理;
C:加大交通违法处罚力度;
D:纳入机动车管理;
E:分时间分路段限行
调查数据的部分统计结果如下表:
管理措施 | 回答人数 | 百分比 |
A | 25 | 5% |
B | 100 | m |
C | 75 | 15% |
D | n | 35% |
E | 125 | 25% |
合计 | a | 100% |
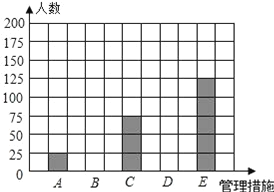
(1)根据上述统计表中的数据可得m=_____,n=_____,a=_____;
(2)在答题卡中,补全条形统计图;
(3)该社区有居民2600人,根据上述调查结果,请你估计选择“D:纳入机动车管理”的居民约有多少人?