题目内容
【题目】如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB. 
(1)求证:直线BF是⊙O的切线;
(2)若点D,点E分别是弧AB的三等分点,当AD=5时,求BF的长;
(3)在(2)的条件下,如果以点C为圆心,r为半径的圆上总存在不同的两点到点O的距离为5,求r的取值范围.
【答案】
(1)证明:如图,∵∠CBF=∠CFB,
∴CB=CF.
又∵AC=CF,
∴CB= ![]() AF,
AF,
∴△ABF是直角三角形,
∴∠ABF=90°,即AB⊥BF.
又∵AB是直径,
∴直线BF是⊙O的切线
(2)解:如图,连接DO,EO,
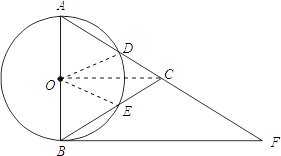
∵点D,点E分别是弧AB的三等分点,
∴∠AOD=60°.
又∵OA=OD,
∴△AOD是等边三角形,
∴OA=AD=OD=5,∠OAD=60°,
∴AB=10.
∴在Rt△ABF中,∠ABF=90°,BF=ABtan60°=10 ![]() ,即BF=10
,即BF=10 ![]()
(3)如图,连接OC.则OC是Rt△ABF的中位线,

∵由(2)知,BF=10 ![]() ,
,
∴圆心距OC= ![]() ,
,
∵⊙O半径OA=5.
∴ ![]() <r<
<r< ![]() .
.
【解析】(1)欲证明直线BF是⊙O的切线,只需证明AB⊥BF;(2)根据圆心角、弧、弦间的关系,等边三角形的判定证得△AOD是等边三角形,所以在Rt△ABF中,∠ABF=90°,∠OAD=60°,AB=10,则利用∠A的正切三角函数的定义来求BF边的长度;(3)根据已知条件知⊙O与⊙C相交.

练习册系列答案
相关题目