Question

【题目】如图，A、B两城市相距80km，现计划在这两座城市间修建一条高速公路（即线段AB），经测量，森林保护中心P在A城市的北偏东30°和B城市的北偏西45°的方向上，已知森林保护区的范围在以P点为圆心，50km为半径的圆形区域内，请问计划修建的这条高速公路会不会穿越保护区，为什么？（参考数据： ≈1.732， ≈1.414）

Answer 1

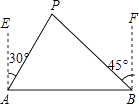
【答案】解：作PM⊥AB，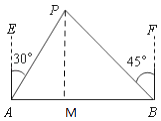

由题意得：AE∥PM∥BF，
∴∠APM=30°，∠BPM=45°，
∴PM= = AM，BM=PM，
设BM=PM=x，则AM= x，
∴
∴x=120﹣40 ≈50.72＞50，
∴这条高速公路不会穿越保护区
【解析】过点P作PM⊥AB，M是垂足．AM与BM就都可以根据三角函数用PPM表示出来．根据AB的长，得到一个关于PM的方程，解出PM的长．从而判断出这条高速公路会不会穿越保护区．
【考点精析】解答此题的关键在于理解解直角三角形的相关知识，掌握解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)．