题目内容
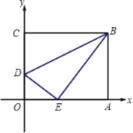
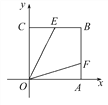
【题目】如图,正方形OABC中,点B(4,4),点E,F分别在边BC,BA上,OE=![]() ,若∠EOF=45°,则OF的解析式为 ( )
,若∠EOF=45°,则OF的解析式为 ( )
A. y=![]() x B. y=
x B. y=![]() x C. y=
x C. y=![]() x D. y=
x D. y=![]() x
x
【答案】B
【解析】作辅助线,构建全等三角形,证明△OCE≌△OAD和△EOF≌△DOF,得EF=FD,设AF=x,在直角△EFB中利用勾股定理列方程求出x=![]() ,根据正方形的边长写出点F的坐标,并求直线OF的解析式.
,根据正方形的边长写出点F的坐标,并求直线OF的解析式.
延长BF至D,使AD=CE,连接OD.
∵四边形OABC是正方形,∴OC=OA,∠OCB=∠OAD,∴△OCE≌△OAD,∴OE=OD,∠COE=∠AOD.
∵∠EOF=45°,∴∠COE+∠FOA=90°﹣45°=45°,∴∠AOD+∠FOA=45°,∴∠EOF=∠FOD.
∵OF=OF,∴△EOF≌△DOF,∴EF=FD,由题意得:OC=4,OE=2![]() ,∴CE=
,∴CE=![]() =2,∴BE=2,设AF=x,则BF=4﹣x,EF=FD=2+x,∴(2+x)2=22+(4﹣x)2,解得:x=
=2,∴BE=2,设AF=x,则BF=4﹣x,EF=FD=2+x,∴(2+x)2=22+(4﹣x)2,解得:x=![]() ,∴F(4,
,∴F(4,![]() ),设OF的解析式为:y=kx,4k=
),设OF的解析式为:y=kx,4k=![]() ,k=
,k=![]() ,∴OF的解析式为:y=
,∴OF的解析式为:y=![]() x.
x.
故选B.


练习册系列答案
相关题目