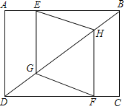
题目内容
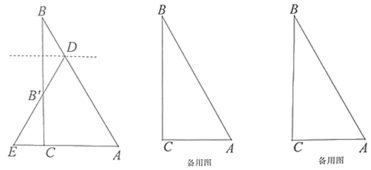
【题目】如图,已知在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在斜边
在斜边![]() 上,将
上,将![]() 沿着过点
沿着过点![]() 的一条直线翻折,使点
的一条直线翻折,使点![]() 落在射线
落在射线![]() 上的点
上的点![]() 处,连接
处,连接![]() 并延长,交射线
并延长,交射线![]() 于
于![]() .
.
(1)当点![]() 与点
与点![]() 重合时,求BD的长.
重合时,求BD的长.
(2)当点![]() 在
在![]() 的延长线上时,设
的延长线上时,设![]() 为
为![]() ,
,![]() 为
为![]() ,求
,求![]() 关于
关于![]() 的函数关系式,并写出定义域.
的函数关系式,并写出定义域.
(3)连接![]() ,当
,当![]() 是直角三角形时,请直接写出
是直角三角形时,请直接写出![]() 的长.
的长.
【答案】(1)1;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)先求出![]() ,当点
,当点![]() 与点
与点![]() 重合时,证得△ACD是等边三角形,解得BD=1;
重合时,证得△ACD是等边三角形,解得BD=1;
(2)过![]() 作
作![]() 于
于![]() ,分别表示出
,分别表示出![]() ,
,![]() ,由
,由![]() ,即可得到y与x的函数解析式;
,即可得到y与x的函数解析式;
(3)分情况分别利用![]() 所对的直角边等于斜边的一半求得AD的长度即可.
所对的直角边等于斜边的一半求得AD的长度即可.
![]() 中,
中,![]() ,
, ![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
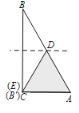
(1)当点![]() 与点
与点![]() 重合时,
重合时, ![]() ,
,
∴△ACD是等边三角形,
∴![]() ;
;
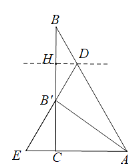
(2)过![]() 作
作![]() 于
于![]() ,
,
![]() 中,
中,![]()
则![]() ,
,![]()
![]() 中,
中,![]()
则![]()
![]()
∴![]()
(3)
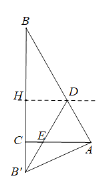
①∵BD=B’D, ![]() ,
,
∴![]() 的情况不成立;
的情况不成立;
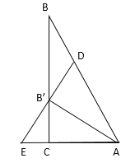
②当![]() 时,如图,
时,如图,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵AB+BD=AB=2,
∴![]() ;
;
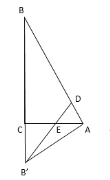
③当![]() 时,如图
时,如图
∵![]() ,
,
∴![]() ,
,
∵BD=B’D,
![]() ,
,
∴![]() ,
,
∴B’D=2AD,即BD=2AD,
∵AD+BD=2,
∴![]() .
.
∴![]() 或
或![]() .
.

练习册系列答案
相关题目