题目内容
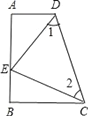
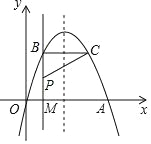
【题目】如图,经过原点的抛物线y=﹣x2+2mx(m>0)与x轴的另一个交点为A,过点P(1,m)作直线PA⊥x轴于点M,交抛物线于点B.记点B关于抛物线对称轴的对称点为C(点B、C不重合),连接CB、CP.
(I)当m=3时,求点A的坐标及BC的长;
(II)当m>1时,连接CA,若CA⊥CP,求m的值;
(III)过点P作PE⊥PC,且PE=PC,当点E落在坐标轴上时,求m的值,并确定相对应的点E的坐标.
【答案】(I)4;(II)![]() (III)(2,0)或(0,4)
(III)(2,0)或(0,4)
【解析】
(I)当m=3时,抛物线解析式为y=-x2+6x,解方程-x2+6x=0得A(6,0),利用对称性得到C(5,5),从而得到BC的长;
(II)解方程-x2+2mx=0得A(2m,0),利用对称性得到C(2m-1,2m-1),再根据勾股定理和两点间的距离公式得到(2m-2)2+(m-1)2+12+(2m-1)2=(2m-1)2+m2,然后解方程即可;
(III)如图,利用△PME≌△CBP得到PM=BC=2m-2,ME=BP=m-1,则根据P点坐标得到2m-2=m,解得m=2,再计算出ME=1得到此时E点坐标;作PH⊥y轴于H,如图,利用△PHE′≌△PBC得到PH=PB=m-1,HE′=BC=2m-2,利用P(1,m)得到m-1=1,解得m=2,然后计算出HE′得到E′点坐标.
(I)当m=3时,抛物线解析式为y=﹣x2+6x,
当y=0时,﹣x2+6x=0,解得x1=0,x2=6,则A(6,0),
抛物线的对称轴为直线x=3,
∵P(1,3),
∴B(1,5),
∵点B关于抛物线对称轴的对称点为C
∴C(5,5),
∴BC=5﹣1=4;
(II)当y=0时,﹣x2+2mx=0,解得x1=0,x2=2m,则A(2m,0),
B(1,2m﹣1),
∵点B关于抛物线对称轴的对称点为C,而抛物线的对称轴为直线x=m,
∴C(2m﹣1,2m﹣1),
∵PC⊥PA,
∴PC2+AC2=PA2,
∴(2m﹣2)2+(m﹣1)2+12+(2m﹣1)2=(2m﹣1)2+m2,
整理得2m2﹣5m+3=0,解得m1=1,m2=![]() ,
,
即m的值为![]() ;
;
(III)如图,
∵PE⊥PC,PE=PC,
∴△PME≌△CBP,
∴PM=BC=2m﹣2,ME=BP=2m﹣1﹣m=m﹣1,
而P(1,m)
∴2m﹣2=m,解得m=2,
∴ME=m﹣1=1,
∴E(2,0);
作PH⊥y轴于H,如图,
易得△PHE′≌△PBC,
∴PH=PB=m﹣1,HE′=BC=2m﹣2,
而P(1,m)
∴m﹣1=1,解得m=2,
∴HE′=2m﹣2=2,
∴E′(0,4);
综上所述,m的值为2,点E的坐标为(2,0)或(0,4).

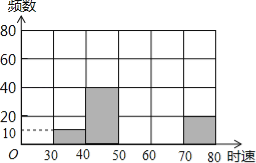
【题目】将某雷达测速区监测到的一组汽车的时速数据整理,得到其频数分布表(未完成):
数据段 | 30~40 | 40~50 | 50~60 | 60~70 | 70~80 | 总计 |
频 数 | 10 | 40 | | | 20 | |
百分比 | 5% | | 40% | | 10% | |
注:30~40为时速大于等于30千米而小于40千米,其他类同.
(1)请你把表中的数据填写完整;
(2)补全频数分布直方图;
(3)如果此路段汽车时速超过60千米即为违章,则违章车辆共有多少辆?