题目内容
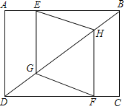
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,点
上,点![]() 、
、![]() 在对角线
在对角线![]() 上,若四边形
上,若四边形![]() 是菱形,则
是菱形,则![]() ________.
________.
【答案】![]()
【解析】
首先连接EF交BD于O,由矩形ABCD中,四边形EGFH是菱形,易证得△DOF≌△BOE(AAS),即可得OB=OD,然后由勾股定理求得BD的长,继而求得OD的长,又由△DOF∽△DCB,利用相似三角形的对应边成比例,即可求得答案.
连接EF交BD于O, 
∵四边形EGFH是菱形,
∴EF⊥BD,OE=OF,
∵四边形ABCD是矩形,
∴∠A=∠C=90°,AB∥CD,AB=DC=4,
∴∠ABO=∠FDO,
在△OEB与△OFD中,∠EBO=∠FDO,∠EOB=∠FOD,OE=OF,
∴△OEB≌△OFD(AAS),
∴BO=DO,
∵AC2=BC2+DC2=32+42=25,
∴BO=![]() AC=
AC=![]() ,
,
∵∠ODF=∠BDC,∠DOF=∠C=90°,
∴△DOF∽△DCB,
∴![]() =
=![]() ∴BE=DF=
∴BE=DF=![]() ,
,
∴AE=ABBE=4![]() =
=![]() ,
,
故答案为:![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目