题目内容
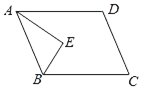
【题目】如图，在ABCD中，点E到AD，AB，BC三边的距离都相等，则∠AEB（ ）
A.是锐角B.是直角C.是钝角D.度数不确定
【答案】B
【解析】
由平行四边形的性质得出∠BAD+∠ABC＝180°，由题意得出AE平分∠BAD，BE平分∠ABC，得出∠BAE＝
∠BAD，∠ABE＝∠ABC，求出∠BAE+∠ABE＝（BAD+∠ABC）＝90°，再由三角形内角和定理即可得出结果．
解：∵四边形ABCD是平行四边形，
∴AD∥BC，
∴∠BAD+∠ABC＝180°，
∵点E到AD，AB，BC三边的距离都相等，
∴AE平分∠BAD，BE平分∠ABC，
∴∠BAE＝∠BAD，∠ABE＝∠ABC，
∴∠BAE+∠ABE＝（BAD+∠ABC）＝×180°＝90°，
∴∠AEB＝90°；
故选：B．
练习册系列答案
开心练习课课练与单元检测系列答案
相关题目
