题目内容
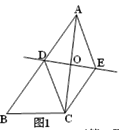
【题目】定义![]() 为一次函数
为一次函数![]() 的特征数.
的特征数.
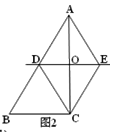
(1)若特征数是![]() 的一次函数为正比例函数,求
的一次函数为正比例函数,求![]() 的值;
的值;
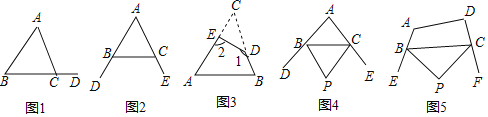
(2)设点![]() 分别为抛物线y=(3x+2m)(x-4)
分别为抛物线y=(3x+2m)(x-4)![]() 与
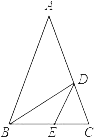
与![]() 轴的交点,其中
轴的交点,其中![]() ,且
,且![]() 的面积为4,
的面积为4,![]() 为原点,求图象过
为原点,求图象过![]() 两点的一次函数的特征数.
两点的一次函数的特征数.
【答案】(1)4;(2) (-12, -8![]() )或(2,-4).
)或(2,-4).
【解析】(1)由题中的新定义[p,q]为一次函数y=px+q的特征数,表示出特征数为[2k+2,3k-12]表示的一次函数,根据一次函数y=kx+b中b=0,列出关于k的方程,求出方程的解即可得到k的值;
(2)先分别求出抛物线与x轴、y轴的交点,然后根据![]() 的面积为4,得到关于m的方程,解方程求得m的值后,确定出A、B两点的坐标,即可求得图象过
的面积为4,得到关于m的方程,解方程求得m的值后,确定出A、B两点的坐标,即可求得图象过![]() 两点的一次函数的特征数.
两点的一次函数的特征数.
(1)根据题意得:特征数为[2k+2,3k-12]的一次函数是y=(2k+2)x+3k-12,
又此一次函数为正比例函数,
∴3k-12=0,解得:k=4;
(2) y=(3x+2m)(x-4)中,令y=0,则有(3x+2m)(x-4)=0,解得:x1=![]() ,x2=4,
,x2=4,
令x=0,则有y=-8m,
所以抛物线与x轴的交点为A1(![]() ,0),A2(4,0),
,0),A2(4,0),
与y轴的交点为B(0,-8m),
若![]() =4,则;4=
=4,则;4=![]() ,因为
,因为![]() ,所以m=
,所以m=![]() ,
,
若![]() =4,则;4=
=4,则;4=![]() ,因为
,因为![]() ,所以m=
,所以m=![]() ,
,
所以满足题设条件,抛物线的解析式为与坐标轴的交点为
A(![]() ,0),B(0,-4
,0),B(0,-4![]() )或A(4,0),B(0,-2),
)或A(4,0),B(0,-2),
利用待定系数法可求得直线AB的解析式为:
y=-12x-4![]() 或y=
或y=![]() x-2,
x-2,
图象过A,B 两点的一次函数的特征数为(-12, -4![]() )或(
)或(![]() ,-2).
,-2).

练习册系列答案
相关题目