Question

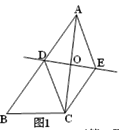
【题目】如图，已知△ABC，AC的垂直平分线交AB于点D，交AC于点O，过点C作CE∥AB交直线OD于点E，连接AE、CD.

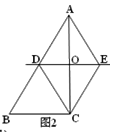
⑴如图1，求证：四边形ADCE是菱形；

⑵如图2，当∠ACB＝90°，BC＝6，△ADC的周长为18时，求AC的长度.

Answer 1

【答案】（1）见解析；（2）AC＝8

【解析】（1）利用直线DE是线段AC的垂直平分线，得出AC⊥DE，即∠AOD=∠COE=90°，进而得出△AOD≌△COE，即可得出四边形ADCE是菱形；

（2）利用当∠ACB=90°时，OD∥BC，即有△ADO∽△ABC，即可得出AC的长．

详（1）证明：∴直线DE是线段AC的垂直平分线，

∴AC⊥DE，即∠AOD=∠COE=90°；

且AD=CD、AO=CO，

又∵CE∥AB，

∴∠1=∠2，

在△AOD和△COE中

，

∴△AOD≌△COE（AAS），

∴OD=OE，

∵A0=CO，DO=EO，

∴四边形ADCE是平行四边形，

又∵AC⊥DE，

∴四边形ADCE是菱形；

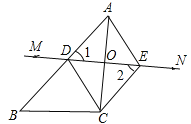
（2）当∠ACB=90°时，OD∥BC，

即有△ADO∽△ABC，

∴，

又∵BC=6，

∴OD=3，

又∵△ADC的周长为18，

∴AD+AO=9，

即AD=9-AO，

∴OD==3，

可得AO=4，

∴AC=8．