题目内容
【题目】如图,将两块直角三角尺的直角顶点C叠放在一起.
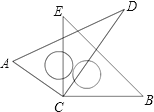
(1)判断∠ACE与∠BCD的大小关系,并说明理由;
(2)若∠DCE=30°,求∠ACB的度数;
(3)猜想:∠ACB与∠DCE有怎样的数量关系,并说明理由.
【答案】(1)∠ACE=∠BCD;(2)150°;(3)∠ACB+∠DCE=180°,见解析
【解析】
试题分析:(1)根据余角的性质,可得答案;
(2)根据余角的定义,可得∠ACE,根据角的和差,可得答案;
(3)根据补角的定义,可得答案.
解:(1)∠ACE=∠BCD,理由如下:
∵∠ACE+∠DCE=90°,∠BCD+∠DCE=90°,
∴∠ACE=∠BCD;
(2)由余角的定义,得∠ACE=90°﹣∠DCE=90°﹣30°=60°,
由角的和差,得∠ACB=∠ACE+∠BCE=60°+90°=150°;
(3)∠ACB+∠DCE=180°,理由如下:
由角的和差,得∠ACB=∠BCE+∠ACE,
∠ACB+∠DCE=∠BCE+(∠ACE+DCE)=∠BCE+∠ACE=180°.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目