��Ŀ����
����Ŀ�����������Ⱦ�Ϊa���߶Σ��ֱ�����Ҫ��Բ��
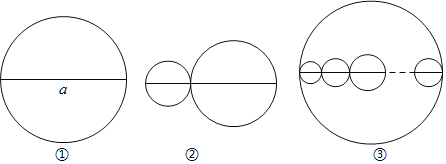
��1����ͼ�����Ը��߶�Ϊֱ����һ��Բ���Ǹ�Բ���ܳ�ΪC1����ͼ�����ڸ��߶�����ȡһ�㣬�ٷֱ�������С�߶�Ϊֱ��������Բ��������Բ���ܳ��ĺ�ΪC2����ָ��C1��C2��������ϵ����˵�����ɣ�
��2����ͼ������a��11ʱ���Ը��߶�Ϊֱ����һ����Բ�����ڴ�Բ�ڻ���ǧСԲ����ЩСԲ��ֱ�����ʹ�Բ��ֱ����ͬһ��ֱ���ϣ���СԲ��ֱ���ĺ͵��ڴ�Բ��ֱ������ôͼ������СԲ���ܳ��ĺ�Ϊ�� ������ֱ����д�𰸣������������
���𰸡���1��C1��C2�����������������2��11����
��������
��1�����߶�a�ֳ�������Ϊa1��a2����a1+a2��a������Բ���ܳ���ʽ![]() �õ�C1����a��C2������a1+a2������a���Ӷ��õ�C1��C2����ȣ�
�õ�C1����a��C2������a1+a2������a���Ӷ��õ�C1��C2����ȣ�
��2����СԲ��ֱ���ֱ�Ϊd1��d2��d3������dn����d1+d2+d3+��+dn��a��11��Ȼ�����Բ���ܳ���ʽ�õ�C1+C2+C3+��+Cn����d1+��d2+��d3+��+��dn������d1+d2+d3+��+dn��=![]() ��������⣮
��������⣮
�⣺��1��C1��C2��
�������£����߶�a�ֳ�������Ϊa1��a2����a1+a2��a��
��C1����a��C2����a1+��a2������a1+a2������a��
��C1��C2��
��2����СԲ��ֱ���ֱ�Ϊd1��d2��d3������dn����d1+d2+d3+��+dn��a��11��
��C1+C2+C3+��+Cn����d1+��d2+��d3+��+��dn������d1+d2+d3+��+dn����11����
�ʴ�Ϊ��11����

 ������ʱͬ����ϰ��ϵ�д�
������ʱͬ����ϰ��ϵ�д�