题目内容
【题目】如图1,已知∠ACD是△ABC的一个外角,我们容易证明∠ACD=∠A+∠B,即三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?
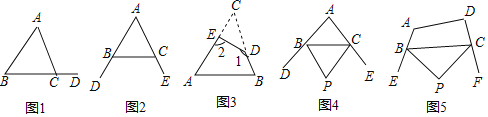
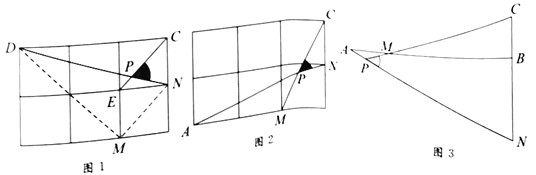
尝试探究:(1)如图2,∠DBC与∠ECB分别为△ABC的两个外角,则∠DBC+∠ECB ∠A+180°(横线上填>、<或=)
初步应用:(2)如图3,在△ABC纸片中剪去△CED,得到四边形ABDE,∠1=135°,则∠2-∠C= .
解决问题:(3)如图4,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请利用上面的结论直接写出答案 .
(4)如图5,在四边形ABCD中,BP、CP分别平分外角∠EBC、∠FCB,请利用上面的结论探究∠P与∠A、∠D的数量关系.
【答案】(1)=;(2)45°;(3)∠P=90°-![]() ∠A;(4)∠P=180°-
∠A;(4)∠P=180°-![]() ∠A-
∠A-![]() ∠D
∠D
【解析】
(1)根据三角形外角的性质可得∠DBC=∠A+∠ACB,∠ECB=∠A+∠ABC,然后求和并根据三角形的内角和定理即可得出结论;
(2)根据(1)的结论即可求出∠2-∠C;
(3)根据(1)的结论可得∠DBC+∠ECB=∠A+180°,然后根据角平分线的定义计算出∠CBP+∠BCP,再根据三角形的内角和定理即可得出结论;
(4)根据四边形的内角和可得∠ABC+∠DCB=360°-∠A-∠D,然后根据平角的定义可推出∠EBC+∠FCB=∠A+∠D,然后根据角平分线的定义和三角形的内角和定理即可得出结论.
解:(1)∵∠DBC与∠ECB分别为△ABC的两个外角
∴∠DBC=∠A+∠ACB,∠ECB=∠A+∠ABC
∴∠DBC+∠ECB=∠A+∠ACB+∠A+∠ABC=∠A+(∠ACB+∠A+∠ABC)=∠A+180°
故答案为:=;
(2)由(1)的结论可知:∠1+∠2=∠C+180°
∵∠1=135°
∴∠2-∠C=180°-∠1=45°
故答案为:45°
(3)由(1)的结论可知:∠DBC+∠ECB=∠A+180°
∵BP、CP分别平分外角∠DBC、∠ECB,
∴∠CBP=![]() ∠DBC,∠BCP=
∠DBC,∠BCP=![]() ∠ECB
∠ECB
∴∠CBP+∠BCP
=![]() ∠DBC+
∠DBC+![]() ∠ECB
∠ECB
=![]() (∠DBC+∠ECB)
(∠DBC+∠ECB)
=![]() (∠A+180°)
(∠A+180°)
=![]() ∠A+90°
∠A+90°
∵∠CBP+∠BCP+∠P=180°
∴∠P=180°-(∠CBP+∠BCP)
=180°-(![]() ∠A+90°)
∠A+90°)
=90°-![]() ∠A
∠A
故答案为:∠P=90°-![]() ∠A
∠A
(4)根据四边形的内角和可得∠ABC+∠DCB=360°-∠A-∠D
∵∠EBC=180°-∠ABC,∠FCB=180°-∠DCB
∴∠EBC+∠FCB
=180°-∠ABC+180°-∠DCB
=360°-(∠ABC+∠DCB)
=360°-(360°-∠A-∠D)
=∠A+∠D
∵BP、CP分别平分外角∠EBC、∠FCB,
∴∠CBP=![]() ∠EBC,∠BCP=
∠EBC,∠BCP=![]() ∠FCB
∠FCB
∴∠CBP+∠BCP
=![]() ∠EBC+
∠EBC+![]() ∠FCB
∠FCB
=![]() (∠EBC+∠FCB)
(∠EBC+∠FCB)
=![]() (∠A+∠D)
(∠A+∠D)
∵∠CBP+∠BCP+∠P=180°
∴∠P=180°-(∠CBP+∠BCP)
=180°-![]() (∠A+∠D)
(∠A+∠D)
=180°-![]() ∠A-
∠A-![]() ∠D
∠D

 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案