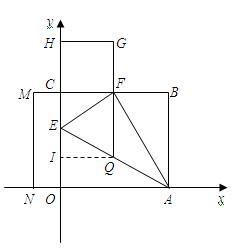
题目内容
如图所示,将矩形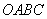 沿
沿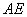 折叠,使点
折叠,使点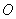 恰好落在
恰好落在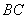 上
上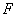 处,以
处,以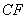 为边作正方形
为边作正方形 ,延长
,延长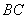 至
至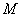 ,使
,使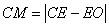 ,再以
,再以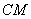 、
、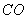 为边作矩形
为边作矩形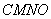 .
.
(1). (2分)试比较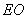 、
、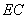 的大小,并说明理由.
的大小,并说明理由.
(2). (1分)令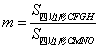 ,请问
,请问 是否为定值?若是,请求出
是否为定值?若是,请求出 的值;若不是,请说明理由.
的值;若不是,请说明理由.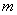 为定值.
为定值.
(3). (3分)在(2)的条件下,若 为
为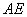 上一点且
上一点且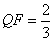 ,抛物线
,抛物线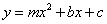 经过
经过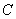 、
、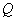 两点,请求出此抛物线的解析式.
两点,请求出此抛物线的解析式.
(4). (4分)在(3)的条件下,若抛物线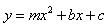 与线段
与线段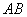 交于点
交于点 ,试问在直线
,试问在直线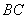 上是否存在点
上是否存在点 ,使得以
,使得以 、
、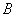 、
、 为顶点的三角形与
为顶点的三角形与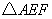 相似?若存在,请求直线
相似?若存在,请求直线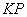 与
与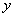 轴的交点
轴的交点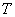 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
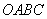 沿
沿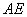 折叠,使点
折叠,使点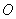 恰好落在
恰好落在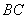 上
上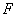 处,以
处,以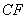 为边作正方形
为边作正方形 ,延长
,延长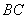 至
至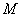 ,使
,使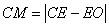 ,再以
,再以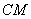 、
、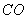 为边作矩形
为边作矩形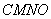 .
.
(1). (2分)试比较
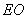 、
、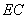 的大小,并说明理由.
的大小,并说明理由.(2). (1分)令
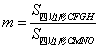 ,请问
,请问 是否为定值?若是,请求出
是否为定值?若是,请求出 的值;若不是,请说明理由.
的值;若不是,请说明理由.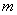 为定值.
为定值.(3). (3分)在(2)的条件下,若
 为
为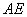 上一点且
上一点且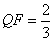 ,抛物线
,抛物线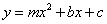 经过
经过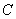 、
、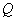 两点,请求出此抛物线的解析式.
两点,请求出此抛物线的解析式.(4). (4分)在(3)的条件下,若抛物线
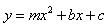 与线段
与线段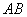 交于点
交于点 ,试问在直线
,试问在直线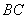 上是否存在点
上是否存在点 ,使得以
,使得以 、
、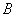 、
、 为顶点的三角形与
为顶点的三角形与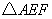 相似?若存在,请求直线
相似?若存在,请求直线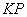 与
与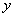 轴的交点
轴的交点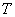 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.(1)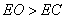 ,理由如下:
,理由如下:
由折叠知: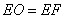 在
在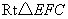 中,
中, 为斜边
为斜边 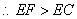
故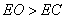
(2)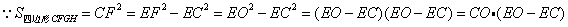
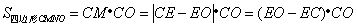
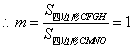
(3)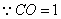 ,
, ,
,
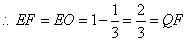
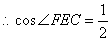
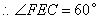
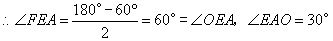
 为等边三角形,
为等边三角形,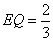
作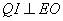 于
于 .
. 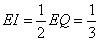
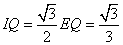
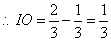
 的坐标为
的坐标为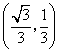
 抛物线
抛物线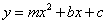 过点
过点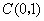 ,
,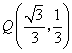 ,
,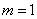
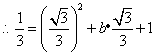
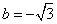
 所求抛物线解析式为
所求抛物线解析式为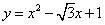
(4)由(3):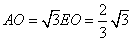
当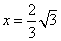 时,
时,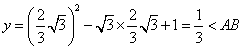
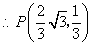
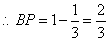
方法1:若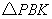 与
与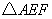 相似,
相似,
而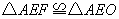 .则分情况如下
.则分情况如下
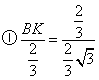 时
时 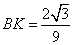
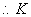 为
为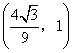 或
或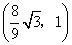
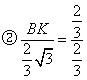 时
时 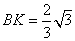
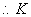 为
为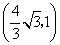 或(0,1)
或(0,1)
故直线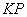 与
与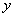 轴交点
轴交点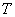 的坐标为
的坐标为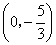 或
或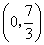 或
或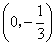 或(0,1)
或(0,1)
方法2: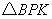 与
与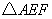 相似时,由(3)得则
相似时,由(3)得则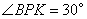 或
或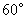 ,
,
过 点作
点作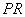 垂直
垂直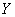 轴于
轴于 则
则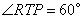 或
或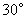
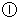 当
当 时,
时,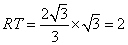
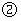 当
当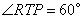
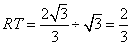
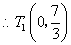 ,
,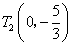
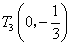 ,
,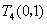
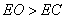 ,理由如下:
,理由如下:由折叠知:
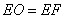 在
在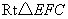 中,
中, 为斜边
为斜边 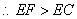
故
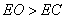
(2)
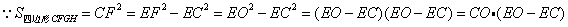
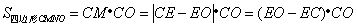
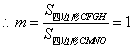
(3)
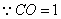 ,
, ,
,
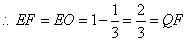
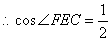
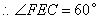
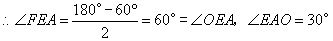
 为等边三角形,
为等边三角形,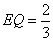
作
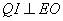 于
于 .
. 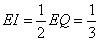
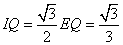
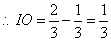
 的坐标为
的坐标为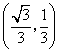
 抛物线
抛物线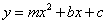 过点
过点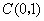 ,
,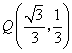 ,
,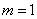
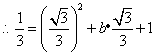
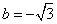
 所求抛物线解析式为
所求抛物线解析式为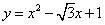
(4)由(3):
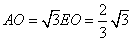
当
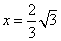 时,
时,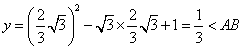
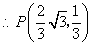
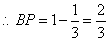
方法1:若
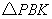 与
与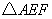 相似,
相似,而
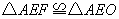 .则分情况如下
.则分情况如下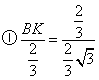 时
时 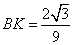
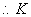 为
为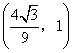 或
或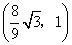
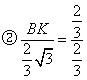 时
时 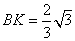
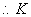 为
为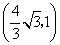 或(0,1)
或(0,1)故直线
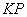 与
与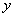 轴交点
轴交点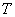 的坐标为
的坐标为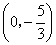 或
或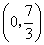 或
或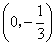 或(0,1)
或(0,1)方法2:
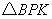 与
与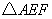 相似时,由(3)得则
相似时,由(3)得则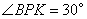 或
或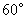 ,
,过
 点作
点作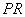 垂直
垂直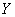 轴于
轴于 则
则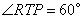 或
或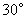
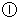 当
当 时,
时,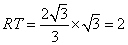
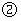 当
当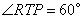
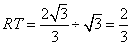
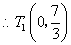 ,
,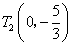
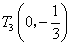 ,
,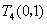
略

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 中,抛物线
中,抛物线 向左平移1个单位,再向下平移4个单位,得到抛物线
向左平移1个单位,再向下平移4个单位,得到抛物线 .所得抛物线与
.所得抛物线与 轴交于
轴交于 两点(点
两点(点 在点
在点 的左边),与
的左边),与 轴交于点
轴交于点 ,顶点为
,顶点为 .
. 的值;
的值; 上是否存在点
上是否存在点 ,使
,使 与
与 相似.若存在,求出点
相似.若存在,求出点

 C. 24 D. 5
C. 24 D. 5  ( ▲ )
( ▲ )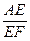 的值.
的值.