题目内容
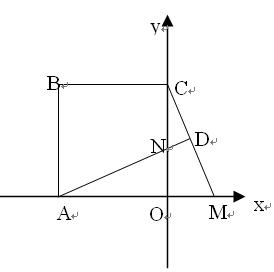
在平行四边形ABCD中,E为CD上一点,DE:EC=1:2,连接AE、BE、BD,且AE、BD交于点F,则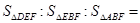 ( ▲ )
( ▲ )
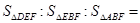 ( ▲ )
( ▲ )| A.1:3:9 | B.1:5:9 | C.2:3:5 | D.2:3:9 |
A
根据已知可得到相似三角形,从而可得到其相似比,再根据相似三角形的面积比等于相似比的平方就可得到答案.
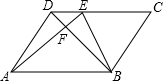
解:由题意得△DFE∽△BFA
∴DE:AB=1:3,DF:FB=1:3
∴S△DEF:S△EBF:S△ABF=1:3:9.
故选A.
本题用到的知识点为:相似三角形的面积比等于相似比的平方,同高的三角形的面积之比等于底的比.

解:由题意得△DFE∽△BFA
∴DE:AB=1:3,DF:FB=1:3
∴S△DEF:S△EBF:S△ABF=1:3:9.
故选A.
本题用到的知识点为:相似三角形的面积比等于相似比的平方,同高的三角形的面积之比等于底的比.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
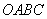 沿
沿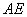 折叠,使点
折叠,使点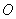 恰好落在
恰好落在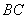 上
上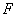 处,以
处,以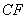 为边作正方形
为边作正方形 ,延长
,延长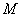 ,使
,使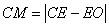 ,再以
,再以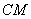 、
、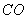 为边作矩形
为边作矩形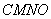 .
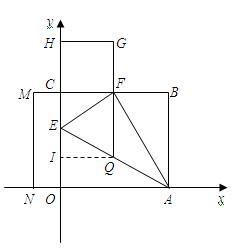
.
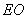 、
、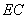 的大小,并说明理由.
的大小,并说明理由.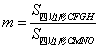 ,请问
,请问 是否为定值?若是,请求出
是否为定值?若是,请求出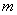 为定值.
为定值. 为
为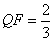 ,抛物线
,抛物线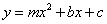 经过
经过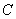 、
、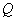 两点,请求出此抛物线的解析式.
两点,请求出此抛物线的解析式.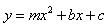 与线段
与线段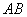 交于点
交于点 ,试问在直线
,试问在直线 ,使得以
,使得以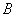 、
、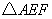 相似?若存在,请求直线
相似?若存在,请求直线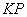 与
与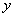 轴的交点
轴的交点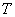 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. ,D、E分别是AB、AC上的点,
,D、E分别是AB、AC上的点, ,如图(1),然后将
,如图(1),然后将 绕A点顺时针旋转
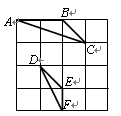
绕A点顺时针旋转 ,使B、A、E三点在同一直线上,得到图(2),M、N分别是BD、CE的中点,连接AM、AN、MN得到图(3),请解答下列问题:
,使B、A、E三点在同一直线上,得到图(2),M、N分别是BD、CE的中点,连接AM、AN、MN得到图(3),请解答下列问题: 与
与
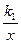 (k1<0,x<0)上一动点,过点P作x轴,y轴的垂线,分别交x轴,y轴于A,B两点,交双曲线y=
(k1<0,x<0)上一动点,过点P作x轴,y轴的垂线,分别交x轴,y轴于A,B两点,交双曲线y=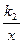 (0<k2<︱k1︱)于E,F两点.
(0<k2<︱k1︱)于E,F两点.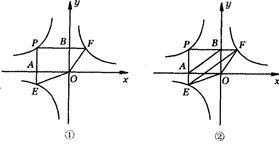
 中,
中,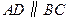 ,
,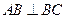 ,以
,以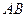 为直径的
为直径的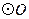 与
与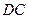 相切于
相切于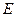 .已知
.已知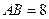 ,边
,边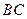 比
比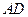 大6.
大6.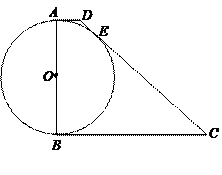
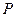 ,使以
,使以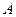 、
、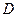 、
、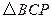 相似?若存在,求出
相似?若存在,求出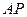 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.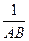 +
+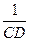 =
=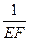 成立,若将图13中的垂直改为斜交,如图14,AB∥CD,AB与BC交于点E,过点E作EF∥AB交BD于F,则
成立,若将图13中的垂直改为斜交,如图14,AB∥CD,AB与BC交于点E,过点E作EF∥AB交BD于F,则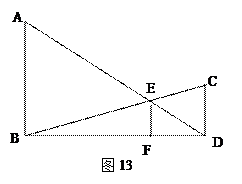



 正确,并说明理由.再直接写出t>0时满足题意的一个点P的坐标.
正确,并说明理由.再直接写出t>0时满足题意的一个点P的坐标.