题目内容
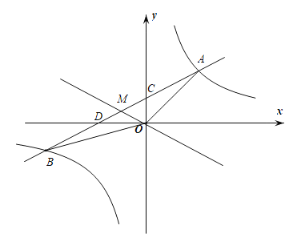
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 相交于
相交于![]() 、
、![]() 两点,与
两点,与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,已知
两点,已知![]() ,
,![]() 的面积为
的面积为![]() .
.
(1)求一次函数和反比例函数的解析式;
(2)连接![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 的中点,直线
的中点,直线![]() 向上平移
向上平移![]() 个单位将
个单位将![]() 的面积分成
的面积分成![]() 两部分,求
两部分,求![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据一函数解析式求得OC的长,在Rt△OCD中,利用三角函数与勾股定理求得OD的长,即D点坐标,然后代入一次函数解析式求得k的值,即可得到一次函数解析式,再根据△BOD的面积求得B点纵坐标,代入一次函数得到B点坐标,然后代入反比例函数即可得解;
(2)先联立方程求得M点坐标,再设向上平移![]() 个单位得到的直线l′为:y=﹣
个单位得到的直线l′为:y=﹣![]() x+h,并设l′与线段AB交于点E,与线段OA交于点F.由题意可知:S△AEF:S△AOB=1:8,即S△AEF:S△AOM=1:4,得到E为AM中点,再将E点坐标代入y=﹣
x+h,并设l′与线段AB交于点E,与线段OA交于点F.由题意可知:S△AEF:S△AOB=1:8,即S△AEF:S△AOM=1:4,得到E为AM中点,再将E点坐标代入y=﹣![]() x+h求得h的值即可.
x+h求得h的值即可.
解:(1)令x=0,则y=1,
∴直线与y轴的交点C(0,1),
∴OC=1,
在Rt△OCD中,
∵![]() ,
,
∴CD=![]() =
=![]() ,
,
∴OD=![]() =2,
=2,
∴D(﹣2,0),
把D(﹣2,0)代入函数![]() ,解得:k=
,解得:k=![]() ,
,
∴一次函数的解析式为:![]() ,
,
又∵S△BOD=![]() ·OD·∣yB∣=1,
·OD·∣yB∣=1,
∴yB=﹣1,
把yB=﹣1代入一次函数得:xB=﹣4,
∴B(﹣4,﹣1),
把B(﹣4,﹣1)代入函数![]() ,解得:m=4,
,解得:m=4,
∴反比例函数的解析式为:![]() ;
;
(2)联立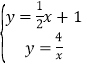 ,
,
解得:![]() 或
或![]() ,
,
∴A(2,2),B(﹣4,﹣1),
∴M(﹣1,![]() ),
),
∴直线OM的解析式为:y=﹣![]() x,
x,
设向上平移![]() 个单位得到的直线l′为:y=﹣
个单位得到的直线l′为:y=﹣![]() x+h,并设l′与线段AB交于点E,与线段OA交于点F.由题意可知:S△AEF:S△AOB=1:8,
x+h,并设l′与线段AB交于点E,与线段OA交于点F.由题意可知:S△AEF:S△AOB=1:8,
∴S△AEF:S△AOM=1:4,
又∵l′与OM平行,
∴E是线段AM的中点,
∴E(![]() ,
,![]() ),
),
把E(![]() ,
,![]() )代入y=﹣
)代入y=﹣![]() x+h得:
x+h得:![]() =﹣
=﹣![]() ×
×![]() +h,
+h,
∴h=![]() .
.