题目内容
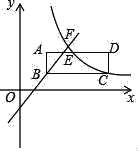
【题目】如图,在平面直角坐标系中,点A、B的坐标分别为(﹣5,0)、(﹣2,0).点P在抛物线y=﹣2x2+4x+8上,设点P的横坐标为m.当0≤m≤3时,△PAB的面积S的取值范围是_____.

【答案】3≤S≤15.
【解析】
根据坐标先求AB的长,所以△PAB的面积S的大小取决于P的纵坐标的大小,因此只要讨论当0≤m≤3时,P的纵坐标的最大值和最小值即可,根据顶点坐标D(1,4),由对称性可知:x=1时,P的纵坐标最大,此时△PAB的面积S最大;当x=3时,P的纵坐标最小,此时△PAB的面积S最小.
∵点A、B的坐标分别为(-5,0)、(-2,0),
∴AB=3,
y=-2x2+4x+8=-2(x-1)2+10,
∴顶点D(1,10),
由图象得:当0≤x≤1时,y随x的增大而增大,
当1≤x≤3时,y随x的增大而减小,
∴当x=3时,即m=3,P的纵坐标最小,
y=-2(3-1)2+10=2,
此时S△PAB=![]() ×2AB=
×2AB=![]() ×2×3=3,
×2×3=3,
当x=1时,即m=1,P的纵坐标最大是10,
此时S△PAB=![]() ×10AB=
×10AB=![]() ×10×3=15,
×10×3=15,
∴当0≤m≤3时,△PAB的面积S的取值范围是3≤S≤15;
故答案为:3≤S≤15.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
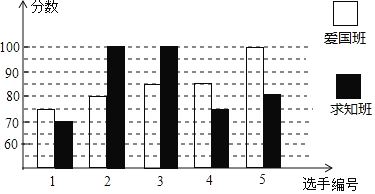
【题目】某校初二开展英语拼写大赛,爱国班和求知班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示:
(1)根据图示填写下表:
班级 | 中位数(分) | 众数(分) | 平均数(分) |
爱国班 | 85 | ||
求知班 | 100 | 85 |
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩比较好?
(3)已知爱国班复赛成绩的方差是70,请求出求知班复赛成绩的方差,并说明哪个班成绩比较稳定?