题目内容
【题目】重庆李子坝轻轨站穿楼而过成网红,小明想要测量轻轨站穿楼时轨道与大楼连接处![]() 距离地面
距离地面![]() 的高度,他站在点
的高度,他站在点![]() 处测得轨道与大楼连接处顶端
处测得轨道与大楼连接处顶端![]() 的仰角为
的仰角为![]() ,向前走了
,向前走了![]() 米到达
米到达![]() 处,再沿着坡度为
处,再沿着坡度为![]() ,长度为
,长度为![]() 米台阶到达
米台阶到达![]() 处,测得轨道与大楼连接处顶端
处,测得轨道与大楼连接处顶端![]() 的仰角为
的仰角为![]() ,已知小明的身高为
,已知小明的身高为![]() 米,则
米,则![]() 的高度约为( )米(精确到
的高度约为( )米(精确到![]() ,参考数据:
,参考数据:![]() ,
,![]() ,
,![]() )
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】
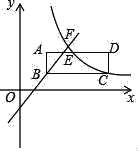
如图,过E点作EH⊥MN的延长线于H,作Rt△BCD,∠D=90°,过点F作FG⊥MN于G,由题意已知,FG=AE=1.6米,∠HEM=45°,∠GFM=53°,在Rt△BCD中,求得CD,BD的长,从而得到AD,NH的长,然后设MN长为x米,在Rt△GMF中,利用三角函数求得GF关于x的关系式,然后在Rt△MHE中,根据MH=HE,得到关于x的方程,然后求解方程即可.
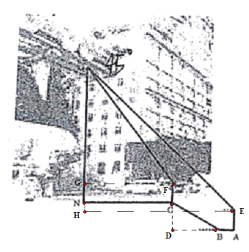
解:如图,过E点作EH⊥MN的延长线于H,作Rt△BCD,∠D=90°,过点F作FG⊥MN于G,由题意已知,FG=AE=1.6米,∠HEM=45°,∠GFM=53°,
∵CD:BD=1:2.4,BC=13m,
∴BD=12m,CD=5m
∵AB=1m,AE=1.6m
∴AD=12+1=13m,NH=5﹣1.6=3.4m
设MN长为x米,
∵∠GFM=53°,
∴∠GMF=37°,
在Rt△GMF中,
![]() =0.75,即GF=0.75·GM=0.75(x﹣1.6),
=0.75,即GF=0.75·GM=0.75(x﹣1.6),
在Rt△MHE中,
∵∠HEM=45°,
∴MH=HE,即MN+NH=GF+AD,
则x+3.4=0.75(x﹣1.6)+13,
解得x=33.6米.
故选:D.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目