题目内容
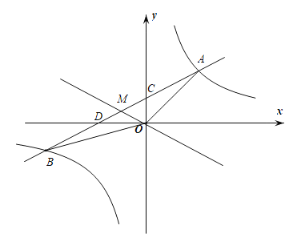
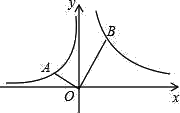
【题目】如图,A,B两点分别在反比例函数y=![]() (x<0)和y=
(x<0)和y=![]() (x>0)的图象上,连接OA,OB,若OA⊥OB,OA=
(x>0)的图象上,连接OA,OB,若OA⊥OB,OA=![]() OB,则k的值为_____.
OB,则k的值为_____.
【答案】﹣![]()
【解析】
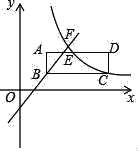
先证得△AEO∽△OFB,根据相似三角形的性质得出OF=3AE,BF=3OE,则OFBF=3AE3OE=9AEOE,得出AEOE=![]() ,设A(a,b),代入y=
,设A(a,b),代入y=![]() (x<0)得出k=ab,因为OE=-a,AE=b,所以AEOE=-ab=-
(x<0)得出k=ab,因为OE=-a,AE=b,所以AEOE=-ab=-![]() .
.
解:如图,过A、B分别作x轴的垂线,垂足分别为E、F.

∵OA⊥OB,
∴∠AOE+∠BOF=90°,
∵∠AOE+∠OAE=90°,
∴∠BOF=∠OAE,
∵∠AEO=∠OFB=90°,
∴△AEO∽△OFB,
![]() =
=![]() ,
,
∴OF=3AE,BF=3OE,
∴OFBF=3AE3OE=9AEOE,
∵B点在反比例函数y=![]() (x>0)的图象上,
(x>0)的图象上,
∴OFBF=9AEOE=3,
∴AEOE=![]() ,
,
设A(a,b),
∵OE=-a,AE=b,
∴AEOE=-ab=![]() ,
,
∴k=ab=-![]() .
.
故答案为-![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
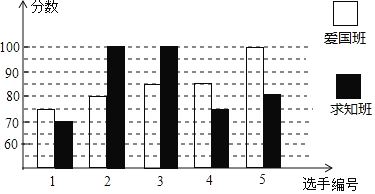
【题目】某校初二开展英语拼写大赛,爱国班和求知班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示:
(1)根据图示填写下表:
班级 | 中位数(分) | 众数(分) | 平均数(分) |
爱国班 | 85 | ||
求知班 | 100 | 85 |
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩比较好?
(3)已知爱国班复赛成绩的方差是70,请求出求知班复赛成绩的方差,并说明哪个班成绩比较稳定?