Question

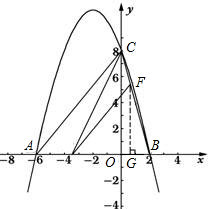
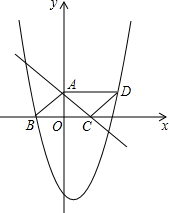
已知抛物线y=ax²+bx+c与x轴交于A、B两点（点B在点A的右侧，且AB=8），与y轴交于点C，其中点A在x轴的负半轴上，点C在y轴的正半轴上，线段OA、OC的长（OA＜OC）是方程x²-14x+48=0的两个根．
（1）求此抛物线的解析式；
（2）连接AC、BC，若点E是线段AB上的一个动点（与点A、点B不重合），过点E作EF∥AC交BC于点F，连接CE，设AE的长为m，△CEF的面积为S，求S与m之间的函数关系式，并写出自变量m的取值范围；
（3）在（2）的基础上试说明S是否存在最大值，若存在，请求出S的最大值，并求出此时点E的坐标，判断此时△BCE的形状；若不存在，请说明理由．

Answer 1

（1）解方程x²-14x+48=0得x₁=6，x₂=8，
由题意得
A（-6，0），C（0，8），B（2，0）…（3分）
∵点C（0，8）在抛物线y=ax²+bx+c的图象上，∴c=8，
将A（-6，0）、B（2，0）代入表达式，得

0=36a-6b+8 0=4a+2b+8

，
　解得

a=- 2 3 b=- 8 3

．
∴所求抛物线的表达式为y=-

2

3

x²-

8

3

x+8；　…（2分）

（2）依题意，AE=m，则BE=8-m，
∵OA=6，OC=8，∴AC=10．
∵EF∥AC，
∴△BEF∽△BAC，
∴

EF

AC

=

BE

AB

即

EF

10

=

8-m

8

，
∴EF=

40-5m

4

．…（1分）
过点F作FG⊥AB，垂足为G，
则sin∠FEG=sin∠CAB=

4

5

，
∴

FG

EF

=

4

5

，
∴FG=

4

5

•

40-5m

4

=8-m，
∴S=S_△BCE-S_△BFE=

1

2

（8-m）×8-

1

2

（8-m）（8-m）
=

1

2

（8-m）（8-8+m）=

1

2

（8-m）m=-

1

2

m²+4m．　…（2分）
自变量m的取值范围是0＜m＜8；　　…（1分）

（3）存在．
理由：∵S=-

1

2

m²+4m=-

1

2

（m-4）²+8且-

1

2

＜0，
∴当m=4时，S有最大值，S_最大值=8．　　…（2分）
∵m=4，∴点E的坐标为（-2，0），
∴△BCE为等腰三角形．　　…（1分）