题目内容
20.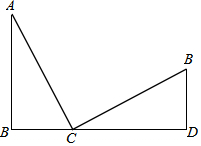 如图,B、C、D三点在同一直线上,∠ABC=∠CDE=90°,且AC⊥EC,BC=DE.
如图,B、C、D三点在同一直线上,∠ABC=∠CDE=90°,且AC⊥EC,BC=DE.(1)求证:△ABC≌△CDE;
(2)若∠BAC=28°,求∠CED的度数.
分析 (1)根据全等三角形的判定定理即可得到结论;
(2)根据全等三角形的性质即可得到结论.
解答 (1)证明:∵∠ABC=∠CDE=90°,且AC⊥EC,
∴∠A+∠ACB=∠ACB+∠ECD=90°,
∴∠A=∠BCD,
在△ABC与△EDC中,$\left\{\begin{array}{l}{∠A=∠BCD}\\{∠ABC=∠CDE}\\{BC=DE}\end{array}\right.$,
∴△ABC≌△CDE;
(2)解:∵△ABC≌△CDE,
∴∠ECD=∠A=28°,
∴∠CED=62°.
点评 本题考查了全等三角形的判定和性质,熟练掌握全等三角形的判定和性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.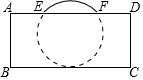 把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=16cm,则球的半径为( )
把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=16cm,则球的半径为( )
 把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=16cm,则球的半径为( )
把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=16cm,则球的半径为( )| A. | 10$\sqrt{3}$cm | B. | 10cm | C. | 10$\sqrt{2}$cm | D. | 8$\sqrt{3}$cm |
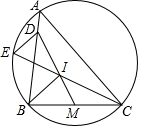 M是BC边的中点,I为内心,连接M、I交AB边于D,连接CI交外接圆于E,证明:$\frac{DE}{EI}$=$\frac{BI}{CI}$.
M是BC边的中点,I为内心,连接M、I交AB边于D,连接CI交外接圆于E,证明:$\frac{DE}{EI}$=$\frac{BI}{CI}$.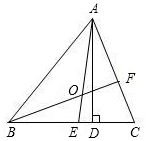 如图所示,在△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=60°,∠C=70°,求∠DAE、∠BOA的度数.
如图所示,在△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=60°,∠C=70°,求∠DAE、∠BOA的度数.