题目内容
10．
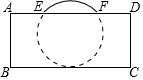把球放在长方体纸盒内，球的一部分露出盒外，其截面如图所示，已知EF=CD=16cm，则球的半径为（ ）| A． | 10$\sqrt{3}$cm | B． | 10cm | C． | 10$\sqrt{2}$cm | D． | 8$\sqrt{3}$cm |
分析 首先找到EF的中点M，作MN⊥AD于点M，取MN上的球心O，连接OF，设OF=x，则OM是16-x，MF=8，然后在直角三角形MOF中利用勾股定理求得OF的长即可．
解答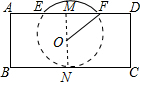 
解：EF的中点M，作MN⊥AD于点M，取MN上的球心O，连接OF，
设OF=x，则OM=16-x，MF=8，
在直角三角形OMF中，OM2+MF2=OF2，
即：（16-x）2+82=x2，
解得：x=10．
故选：B．
点评 本题考查了垂径定理及勾股定理的知识，解题的关键是正确的作出辅助线构造直角三角形．
练习册系列答案
全优测试卷系列答案
冲刺100分1号卷系列答案
相关题目
20．某电子商投产一种新型电子产品，每件制造成本为20元，在销售过程中发现，每月销量y（万件）与销售单价x（元）之间关系如表所示：
（1）求每月的利润W（万元）与销售单价x（元）之间函数解析式；
（2）当销售单价为多少元时，厂商每月能够获得最大利润？最大利润是多少？
| 销售单价x（元） | 21 | 22 | 23 | 24 | 25 | 26 |
| 月销量y（万件） | 18 | 16 | 14 | 12 | 10 | 8 |
（2）当销售单价为多少元时，厂商每月能够获得最大利润？最大利润是多少？
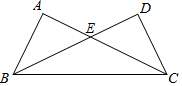如图，在△ABC和△DCB中，AB=DC，AC与BD相交于点E，若不再添加任何字母与辅助线，要使△ABC≌△DCB，则还需增加的一个条件AC=BD．
阅读材料，解答问题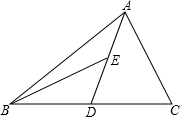
如图，AD为△ABC的中线，BE 为△ABD的中线．
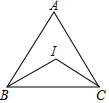正△ABC的两条角平分线BD和CE交于点I，则∠BIC等于120°．
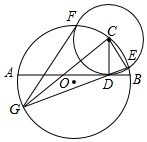如图，AB是⊙O的直径，点C在⊙O上，⊙C与AB相切于点D，交⊙O于E、F两点，连接ED并延长交⊙O于G点，连接CG、FG．
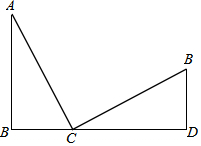如图，B、C、D三点在同一直线上，∠ABC=∠CDE=90°，且AC⊥EC，BC=DE．