题目内容
8.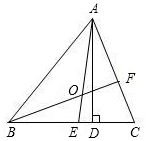 如图所示,在△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=60°,∠C=70°,求∠DAE、∠BOA的度数.
如图所示,在△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=60°,∠C=70°,求∠DAE、∠BOA的度数.
分析 根据垂直的定义、角平分线的定义、三角形内角和定理计算即可.
解答 解∵AD⊥BC,
∴∠ADC=90°,
∵∠C=70°,
∴∠CAD=180°-90°-70°=20°,
∵∠BAC=60°,AE是∠BAC的角平分线,
∴∠EAC=∠BAE=30°,
∴∠EAD=∠EAC-∠CAD=30°-20°=10°,
∠ABC=180°-∠BAC-∠C=50°,
∵BF是∠ABC的角平分线,
∴∠ABO=25°,
∴∠BOA=180°-∠BAO-∠ABO=180°-30°-25°=125°.
故∠DAE,∠BOA的度数分别是10°,125°.
点评 本题考查的是三角形内角和定理、三角形的高和角平分线的定义,掌握三角形内角和等于180°是解题的关键.

练习册系列答案
相关题目
3.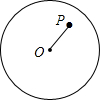 如图,点P为⊙O内一点,且OP=6,若⊙O的半径为10,则过点P的弦长不可能为( )
如图,点P为⊙O内一点,且OP=6,若⊙O的半径为10,则过点P的弦长不可能为( )
 如图,点P为⊙O内一点,且OP=6,若⊙O的半径为10,则过点P的弦长不可能为( )
如图,点P为⊙O内一点,且OP=6,若⊙O的半径为10,则过点P的弦长不可能为( )| A. | 12 | B. | 16 | C. | 17.5 | D. | 20 |
 阅读材料,解答问题
阅读材料,解答问题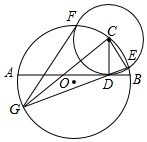 如图,AB是⊙O的直径,点C在⊙O上,⊙C与AB相切于点D,交⊙O于E、F两点,连接ED并延长交⊙O于G点,连接CG、FG.
如图,AB是⊙O的直径,点C在⊙O上,⊙C与AB相切于点D,交⊙O于E、F两点,连接ED并延长交⊙O于G点,连接CG、FG.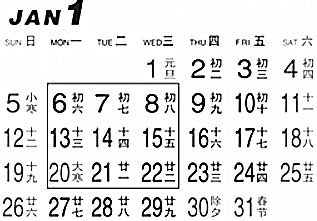 如图是某月的日历表,在此日历表上可以用一个矩形圈出3×3个位置的9个数(如6,7,8,13,14,15,20,21,22),若圈出的9个数中,最大数与最小数的和为46,则这9个数的和为207.
如图是某月的日历表,在此日历表上可以用一个矩形圈出3×3个位置的9个数(如6,7,8,13,14,15,20,21,22),若圈出的9个数中,最大数与最小数的和为46,则这9个数的和为207.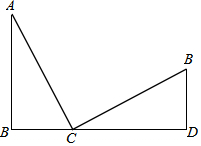 如图,B、C、D三点在同一直线上,∠ABC=∠CDE=90°,且AC⊥EC,BC=DE.
如图,B、C、D三点在同一直线上,∠ABC=∠CDE=90°,且AC⊥EC,BC=DE.