题目内容
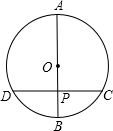
若圆的半径为3，圆中一条弦为2
，则此弦中点到弦所对劣弧的中点的距离为______．
| 5 |
如图：连接OA，OB，则OA=OB=3，
过O作OF垂直AB于E，与圆相交于F，
由垂径定理得：AE=EB=
AB=
×2
=
，
且
=
在Rt△OEB中，OB=3，EB=
，OE=
=
=2，
即这条弦的中点到弦所对劣弧的中点的距离EF=OF-OE=3-2=1．
故答案为：1．
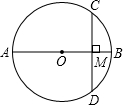
过O作OF垂直AB于E，与圆相交于F，
由垂径定理得：AE=EB=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 5 |
且
 |
| AF |
|
| FB |
在Rt△OEB中，OB=3，EB=
| 5 |
| OB2-EB2 |
32-(
|
即这条弦的中点到弦所对劣弧的中点的距离EF=OF-OE=3-2=1．
故答案为：1．
练习册系列答案
相关题目
