题目内容
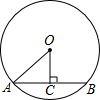
如图,⊙O的直径AB垂直于弦CD,垂足P是OB的中点,CD=2
cm,
求:(1)直径AB的长.
(2)弓形DBC的面积.(结果保留π)

| 3 |
求:(1)直径AB的长.
(2)弓形DBC的面积.(结果保留π)

(1)连接OC,如图,
∵⊙O的直径AB垂直于弦CD,
∴PC=PD,
∵CD=2
,
∴PC=
,
又∵P是OB的中点,
∴OP=
OB=
OC,
在Rt△OPC中,OP2+PC2=OC2,
(
OC)2+(
)2=OC2,
∴OC=2,
∴AB=2OC=4(cm);
(2)在Rt△OPC中,
∵OP=
OC,
∴∠C=30°,
∴∠COP=60°,
∴∠COD=120°,
∴S扇形OCD=
=
;
∵S△COD=
CD•OP=
×2
×1=
,
∴S弓形DBC=S扇形OCD-S△COD=
-
(cm2).

∵⊙O的直径AB垂直于弦CD,
∴PC=PD,
∵CD=2
| 3 |
∴PC=
| 3 |
又∵P是OB的中点,
∴OP=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△OPC中,OP2+PC2=OC2,
(
| 1 |
| 2 |
| 3 |
∴OC=2,
∴AB=2OC=4(cm);
(2)在Rt△OPC中,
∵OP=
| 1 |
| 2 |
∴∠C=30°,
∴∠COP=60°,
∴∠COD=120°,
∴S扇形OCD=
| 120•π×22 |
| 360 |
| 4π |
| 3 |
∵S△COD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
∴S弓形DBC=S扇形OCD-S△COD=
| 4π |
| 3 |
| 3 |


练习册系列答案
相关题目