题目内容
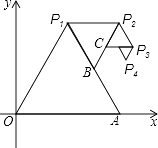
【题目】某天放学后,小红步行,小丽骑自行车沿同一条笔直的马路到图书馆看书,图中线段OA、BC分别表示小红、小丽离开学校的路程s(米)与小红所用的时间t(分钟)的函数关系,根据图象解答下列问题:
(1)小丽比小红迟出发 分钟,小红步行的速度是 米/分钟;(直接写出结果)
(2)两人在路上相距不超过200米的时间有多少分钟?

【答案】(1)5,100;(2)4分钟
【解析】
(1)由点B的横坐标可得出小丽比小红迟出发5分钟;根据速度=路程÷时间,可求出小红步行的速度;
(2)根据点A、B、C的坐标,利用待定系数法可求出线段OA、BC的表达式,分相遇前及相遇后两种情况考虑,令两人之间的距离为200米,可求出两人正好相距200米的时间,二者做差即可求出结论.
解:(1)小丽比小红迟出发5分钟;
小红步行的速度为2000÷20=100(米/分钟).
故答案为:5;100;
(2)由图象知A(20,2000),B(5,0),C(15,2000),
设线段OA的函数表达式为s=kt(k≠0),
把A(20,2000)代入s=kt,得:2000=20k,
解得:k=100,
∴线段OA的函数表达式为s=100t(0≤t≤20);
设线段BC的函数表达式为s=mt+n(m≠0),
把B(5,0),C(15,2000)代入s=mt+n,得:
![]() ,解得:
,解得:![]() ,
,
∴线段BC的函数表达式为s=200t﹣1000(5≤t≤15),
若两人相遇前相距200米,则100t﹣(200t﹣1000)=200,
解得:t=8;
若两人相遇后相距200米,则(200t﹣1000)﹣100t=200,
解得:t=12,
∴12﹣8=4(分钟),
答:两人在路上相距不超过200米的时间有4分钟.

练习册系列答案
相关题目