题目内容
【题目】某年级共有![]() 名学生.为了解该年级学生
名学生.为了解该年级学生![]() ,
,![]() 两门课程的学习情况,从中随机抽取
两门课程的学习情况,从中随机抽取![]() 名学生进行测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理描述和分析下面给出了部分信息.
名学生进行测试,获得了他们的成绩(百分制),并对数据(成绩)进行整理描述和分析下面给出了部分信息.
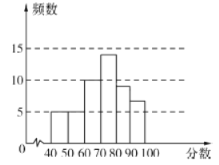
①![]() 课程成绩的频数分布直方图如下(数据分成
课程成绩的频数分布直方图如下(数据分成![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() );
);
②![]() 课程成绩在
课程成绩在![]() 这一组的数据为:
这一组的数据为:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
③![]() ,
,![]() 两门课程成绩的平均数、中位数、众数如下:
两门课程成绩的平均数、中位数、众数如下:
课程 | 平均数 | 中位数 | 众数 |
|
|
|
|
|
|
|
|
根据以上信息,回答下列问题:
(1)写出表中![]() 的值;
的值;
(2)在此次测试中,某学生的![]() 课程成绩为
课程成绩为![]() 分,
分,![]() 课程成绩为
课程成绩为![]() 分,这名学生成绩排名更靠前的课程是_______(填“
分,这名学生成绩排名更靠前的课程是_______(填“![]() ”或“
”或“![]() ”),理由是;___________;
”),理由是;___________;
(3)假设该年级学生都参加了此次测试,估计![]() 课程成绩超过
课程成绩超过![]() 分的人数.
分的人数.
【答案】(1)![]() ;(2)
;(2)![]() 该学生
该学生![]() 课程分数低于中位数,排名在中间位置之后,而
课程分数低于中位数,排名在中间位置之后,而![]() 课程分数高于中位数,排名在中间位置之前;(3)估计
课程分数高于中位数,排名在中间位置之前;(3)估计![]() 课程成绩超过
课程成绩超过![]() 分的人数为
分的人数为![]() .
.
【解析】
(1)先确定A课程的中位数落在第4小组,再由此分组具体数据得出第25、26个数据的平均数即可;
(2)根据两个课程的中位数定义即可解答;
(3)用总人数乘以样本中超过75.8分的人数所占比例可得.
解:(1)![]() ;
;
(2)![]() 该学生
该学生![]() 课程分数低于中位数,排名在中间位置之后,而
课程分数低于中位数,排名在中间位置之后,而![]() 课程分数高于中位数,排名在中间位置之前.
课程分数高于中位数,排名在中间位置之前.
(3)抽取的![]() 名学生中,
名学生中,![]() 课程成绩超过
课程成绩超过![]() 分的人数为
分的人数为![]()
![]() (人).
(人).
故估计![]() 课程成绩超过
课程成绩超过![]() 分的人数为
分的人数为![]() .
.

 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
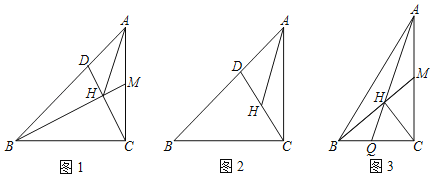
单元期中期末卷系列答案【题目】如图,A,B,C为⊙O上的定点.连接AB,AC,M为AB上的一个动点,连接CM,将射线MC绕点M顺时针旋转90°,交⊙O于点D,连接BD.若AB=6cm,AC=2cm,记A,M两点间距离为xcm,B,D两点间的距离为ycm.
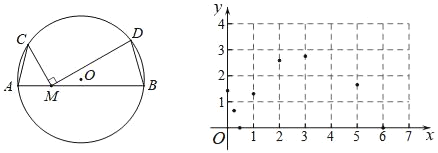
小东根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究.
下面是小东探究的过程,请补充完整:
(1)通过取点、画图、测量,得到了x与y的几组值,如下表,补全表格:
x/cm | 0 | 0.25 | 0.47 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 1.43 | 0.66 | 0 | 1.31 | 2.59 | 2.76 |
| 1.66 | 0 |
(2)在平面直角坐标系xOy中,描出补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:当BD=AC时,AM的长度约为 cm.