ЬтФПФкШн
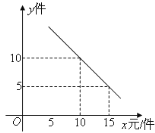
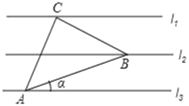
ЁОЬтФПЁПШчЭМХзЮяЯп![]() гыxжсНЛгкЕуA(-1ЃЌ0)ЃЌЖЅЕузјБъ(1ЃЌn)ЃЌгыyжсЕФНЛЕудк(0ЃЌ2)ЃЌ(0ЃЌ3)жЎМфЃЈВЛАќКЌЖЫЕуЃЉЃЌдђЯТСаНсТлЃКЂйa+b=0ЃЛЂк
гыxжсНЛгкЕуA(-1ЃЌ0)ЃЌЖЅЕузјБъ(1ЃЌn)ЃЌгыyжсЕФНЛЕудк(0ЃЌ2)ЃЌ(0ЃЌ3)жЎМфЃЈВЛАќКЌЖЫЕуЃЉЃЌдђЯТСаНсТлЃКЂйa+b=0ЃЛЂк![]() ЃЛЂлШєЕу(-2ЃЌy1)ЃЌ
ЃЛЂлШєЕу(-2ЃЌy1)ЃЌ![]() ЃЌ(2ЃЌy3)дкДЫХзЮяЯпЩЯЃЌдђy1ЃМy2ЃМy3ЃЛЂмЕБ1<x<3ЪБЃЌзмгаax2+bx+c>0ЃЛЂнЙигкxЕФЗНГЬax2+bx+c=n-1гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЎе§ШЗЕФЪЧЃЈ ЃЉ
ЃЌ(2ЃЌy3)дкДЫХзЮяЯпЩЯЃЌдђy1ЃМy2ЃМy3ЃЛЂмЕБ1<x<3ЪБЃЌзмгаax2+bx+c>0ЃЛЂнЙигкxЕФЗНГЬax2+bx+c=n-1гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЎе§ШЗЕФЪЧЃЈ ЃЉ
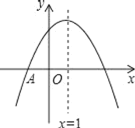
A.ЂйЂкЂмЂнB.ЂйЂкЂлЂмC.ЂмЂнD.ЂкЂлЂмЂн
ЁОД№АИЁПC
ЁОНтЮіЁП
РћгУХзЮяЯпПЊПкЗНЯђЕУЕН![]() ЃЌдйгЩХзЮяЯпЕФЖдГЦжсЗНГЬЕУЕН
ЃЌдйгЩХзЮяЯпЕФЖдГЦжсЗНГЬЕУЕН![]() ЃЌдђ
ЃЌдђ![]() ЃЌПЩЖдЂйНјааХаЖЯЃЛРћгУХзЮяЯп
ЃЌПЩЖдЂйНјааХаЖЯЃЛРћгУХзЮяЯп![]() гыyжсЕФНЛЕудк(0ЃЌ2)ЃЌ(0ЃЌ3)жЎМфЃЈВЛАќКЌЖЫЕуЃЉЃЌЕУЕН
гыyжсЕФНЛЕудк(0ЃЌ2)ЃЌ(0ЃЌ3)жЎМфЃЈВЛАќКЌЖЫЕуЃЉЃЌЕУЕН![]() ЃЌ
ЃЌ ![]() ПЩЖдЂкНјааХаЖЯЃЛРћгУЖўДЮКЏЪ§ЕФаджЪПЩЖдЂлНјааХаЖЯЃЛИљОнХзЮяЯп
ПЩЖдЂкНјааХаЖЯЃЛРћгУЖўДЮКЏЪ§ЕФаджЪПЩЖдЂлНјааХаЖЯЃЛИљОнХзЮяЯп![]() ЕФЭМЯёПЩЖдЂмНјааХаЖЯЃЛИљОнХзЮяЯп
ЕФЭМЯёПЩЖдЂмНјааХаЖЯЃЛИљОнХзЮяЯп![]() гыжБЯп
гыжБЯп![]() гаСНИіНЛЕуПЩЖдЂнНјааХаЖЯЃЎ
гаСНИіНЛЕуПЩЖдЂнНјааХаЖЯЃЎ
НтЃК![]() ХзЮяЯпПЊПкЯђЯТЃЌ
ХзЮяЯпПЊПкЯђЯТЃЌ
![]() ЃЌ
ЃЌ
ЖјХзЮяЯпЕФЖдГЦжсЮЊжБЯп![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
![]() ЃЌЫљвдЂйВЛе§ШЗЃЛ
ЃЌЫљвдЂйВЛе§ШЗЃЛ
ЁпХзЮяЯп![]() гыyжсЕФНЛЕудк(0ЃЌ2)ЃЌ(0ЃЌ3)жЎМфЃЈВЛАќКЌЖЫЕуЃЉЃЌ
гыyжсЕФНЛЕудк(0ЃЌ2)ЃЌ(0ЃЌ3)жЎМфЃЈВЛАќКЌЖЫЕуЃЉЃЌ
Ёр![]() ЃЌ
ЃЌ
Аб![]() ЃЌ
ЃЌ![]() ДјШы
ДјШы![]() ЃЌ
ЃЌ
ЕУ![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌЫљвдЂкВЛе§ШЗЃЛ
ЃЌЫљвдЂкВЛе§ШЗЃЛ
![]() ХзЮяЯпЕФЖЅЕузјБъ
ХзЮяЯпЕФЖЅЕузјБъ![]() ЃЌгыxжсНЛгкЕуA(-1ЃЌ0)ЃЌЕу(-2ЃЌy1)ЃЌ
ЃЌгыxжсНЛгкЕуA(-1ЃЌ0)ЃЌЕу(-2ЃЌy1)ЃЌ![]() ЃЌ(2ЃЌy3)дкДЫХзЮяЯпЩЯЃЌ
ЃЌ(2ЃЌy3)дкДЫХзЮяЯпЩЯЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()
Ёр![]() ЃЌЫљвдЂлВЛе§ШЗЃЛ
ЃЌЫљвдЂлВЛе§ШЗЃЛ
![]() ХзЮяЯпЕФЖЅЕузјБъ
ХзЮяЯпЕФЖЅЕузјБъ![]() ЃЌгыxжсНЛгкЕуA(-1ЃЌ0)ЃЌ
ЃЌгыxжсНЛгкЕуA(-1ЃЌ0)ЃЌ
дђХзЮяЯпгыxжсЕФ СэвЛИіНЛЕуЮЊЃЈ3ЃЌ0ЃЉ
ЁрЕБ1<x<3ЪБЃЌзмгаax2+bx+c>0ЃЌЫљвдЂме§ШЗЃЛ
![]() ХзЮяЯпЕФЖЅЕузјБъ
ХзЮяЯпЕФЖЅЕузјБъ![]() ЃЌ
ЃЌ
![]() ХзЮяЯп
ХзЮяЯп![]() гыжБЯп
гыжБЯп![]() гаСНИіНЛЕуЃЌ
гаСНИіНЛЕуЃЌ
![]() Йигк
Йигк![]() ЕФЗНГЬ
ЕФЗНГЬ![]() гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌЫљвдЂне§ШЗЃЛ
гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌЫљвдЂне§ШЗЃЛ
злЩЯЫљЪіЃЌе§ШЗЕФгаЃКЂмЂн
ЙЪбЁЃКCЃЎ

 аФЫуПкЫуЧЩЫувЛПЮвЛСЗЯЕСаД№АИ
аФЫуПкЫуЧЩЫувЛПЮвЛСЗЯЕСаД№АИЁОЬтФПЁПФГФъМЖЙВга![]() УћбЇЩњЃЎЮЊСЫНтИУФъМЖбЇЩњ
УћбЇЩњЃЎЮЊСЫНтИУФъМЖбЇЩњ![]() ЃЌ
ЃЌ![]() СНУХПЮГЬЕФбЇЯАЧщПіЃЌДгжаЫцЛњГщШЁ
СНУХПЮГЬЕФбЇЯАЧщПіЃЌДгжаЫцЛњГщШЁ![]() УћбЇЩњНјааВтЪдЃЌЛёЕУСЫЫћУЧЕФГЩМЈЃЈАйЗжжЦЃЉЃЌВЂЖдЪ§ОнЃЈГЩМЈЃЉНјааећРэУшЪіКЭЗжЮіЯТУцИјГіСЫВПЗжаХЯЂЃЎ
УћбЇЩњНјааВтЪдЃЌЛёЕУСЫЫћУЧЕФГЩМЈЃЈАйЗжжЦЃЉЃЌВЂЖдЪ§ОнЃЈГЩМЈЃЉНјааећРэУшЪіКЭЗжЮіЯТУцИјГіСЫВПЗжаХЯЂЃЎ
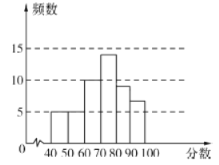
Ђй![]() ПЮГЬГЩМЈЕФЦЕЪ§ЗжВМжБЗНЭМШчЯТЃЈЪ§ОнЗжГЩ
ПЮГЬГЩМЈЕФЦЕЪ§ЗжВМжБЗНЭМШчЯТЃЈЪ§ОнЗжГЩ![]() зщЃК
зщЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()
![]() ЃЉЃЛ
ЃЉЃЛ
Ђк![]() ПЮГЬГЩМЈдк
ПЮГЬГЩМЈдк![]() етвЛзщЕФЪ§ОнЮЊЃК
етвЛзщЕФЪ§ОнЮЊЃК
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ђл![]() ЃЌ
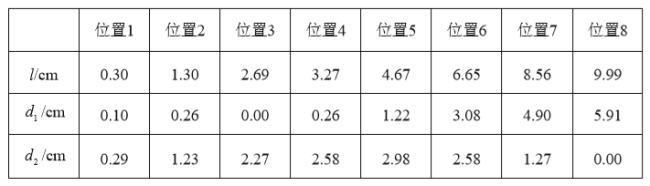
ЃЌ![]() СНУХПЮГЬГЩМЈЕФЦНОљЪ§ЁЂжаЮЛЪ§ЁЂжкЪ§ШчЯТЃК
СНУХПЮГЬГЩМЈЕФЦНОљЪ§ЁЂжаЮЛЪ§ЁЂжкЪ§ШчЯТЃК
ПЮГЬ | ЦНОљЪ§ | жаЮЛЪ§ | жкЪ§ |
|
|
|
|
|
|
|
|
ИљОнвдЩЯаХЯЂЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉаДГіБэжа![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉдкДЫДЮВтЪджаЃЌФГбЇЩњЕФ![]() ПЮГЬГЩМЈЮЊ
ПЮГЬГЩМЈЮЊ![]() ЗжЃЌ
ЗжЃЌ![]() ПЮГЬГЩМЈЮЊ
ПЮГЬГЩМЈЮЊ![]() ЗжЃЌетУћбЇЩњГЩМЈХХУћИќППЧАЕФПЮГЬЪЧ_______ЃЈЬюЁА
ЗжЃЌетУћбЇЩњГЩМЈХХУћИќППЧАЕФПЮГЬЪЧ_______ЃЈЬюЁА![]() ЁБЛђЁА
ЁБЛђЁА![]() ЁБЃЉЃЌРэгЩЪЧЃЛ___________ЃЛ
ЁБЃЉЃЌРэгЩЪЧЃЛ___________ЃЛ
ЃЈ3ЃЉМйЩшИУФъМЖбЇЩњЖМВЮМгСЫДЫДЮВтЪдЃЌЙРМЦ![]() ПЮГЬГЩМЈГЌЙ§
ПЮГЬГЩМЈГЌЙ§![]() ЗжЕФШЫЪ§ЃЎ
ЗжЕФШЫЪ§ЃЎ