题目内容
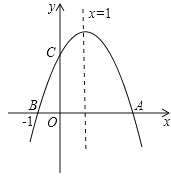
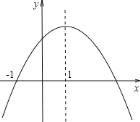
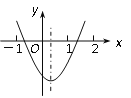
【题目】如图,抛物线y=ax2+bx+c的对称轴是![]() ,小亮通过观察得出了下面四条信息:
,小亮通过观察得出了下面四条信息:
①c<0,②abc<0,③a-b+c>0,④2a-3b=0.你认为其中正确的有________.(填序号)
【答案】①③.
【解析】
利用二次函数的图形和性质,结合抛物线的开口方向,对称轴,以及抛物线与坐标轴的交点对每个命题进行判断.
解:当x=0时,y=c,因为抛物线与y轴的交点在y轴的负半轴,所以c<0,故①正确.
∵抛物线的开口向上,
∴a>0.
∵对称轴x=-![]() =
=![]() ,
,
∴b=-![]() <0.
<0.
∴abc>0.故②错误.
当x=-1时,y=a-b+c,由图形可知:a-b+c>0,故③正确.
由对称轴得:-![]() =
=![]() ,
,
∴2a+3b=0.而不是2a-3b=0,故④错误.
故答案是:①③.
本题考查的是二次函数的图形与系数的关系,由开口方向得到a的正负,由抛物线与y轴的交点得到c的正负,由对称轴得到b的正负,再用抛物线与x的交点得到a-b+c>0,对所给的四个命题作出判断.

练习册系列答案
相关题目