题目内容
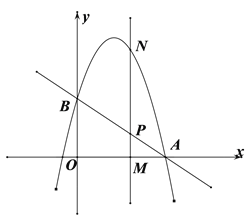
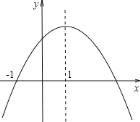
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出下列结论:① b2-4ac>0;② 2a+b<0;③ 4a-2b+c=0;④ a︰b︰c= -1︰2︰3.其中正确的是【 】
(A) ①② (B) ②③ (C) ③④ (D)①④
【答案】D。
【解析】根据二次函数图象和性质分别作出判断:
∵二次函数图象与x轴有两个交点,∴对应的一元二次方程ax2+bx+c 有两个不相等的实数根。
∴b2-4ac>0。选项①正确。
又∵对称轴为直线x=1,即![]() ,∴2a+b=0。选项②错误。
,∴2a+b=0。选项②错误。
∵由图象知,x=-2对应的函数值为负数,∴当x=-2时,y=4a-2b+c<0。选项③错误。
∵图象知,x=-1对应的函数值为0,∴当x=-1时,y=a+b+c=0。
联立2a+b=0和y=a+b+c=0可得:b=-2a,c=-3a。
∴a:b:c=a:(-2a):(-3a)=-1:2:3。选项④正确。
综上所述,正确的选项有:①④。故选D。

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
【题目】如图,某项研究表明,大拇指与小拇指尽量张开时,两指尖的距离称为指距.如表是测得的指距与身高的一组数据:
指距d(cm) | 19 | 20 | 21 |
身高h(cm) | 151 | 160 | 169 |
(1)你能确定身高h与指距d之间的函数关系式吗?
(2)若某人的身高为196cm,一般情况下他的指距应是多少?