题目内容
【题目】P是△ABC的内心，BC=4，∠BAC=90°,则△PBC的外接圆半径为________．
【答案】
【解析】
作如下所示图，先求出∠BPC的度数，再利用圆内接四边形对角互补求出∠BQC的度数，再由圆周角定理求出∠BOC度数，进而得到△BOC是等腰直角三角形，进而求解.
解：作如下所示图，P为△ABC的内心，圆O为△PBC的外接圆，∠BAC=90°
由内心的定义可知，BP、CP、AP分别是∠ABC、∠ACB、∠BAC的角平分线，
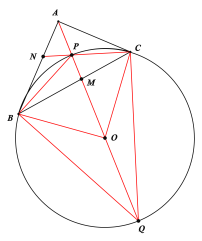
∴∠BPC=180°-(∠PBC+∠PCB)=180°-(
∠ABC+∠ACB)
=180°-(∠ABC+∠ACB)
=180°-(180°-∠BAC)=180°-×90°=135°.
由圆内接四边形对角互补知：∠BQC+∠BPC=180°
∴∠BQC=180°-∠BPC=45°
由同弧所对的圆周角等于圆心角的一半知：
∠BOC=2∠BQC=90°
且BO=CO，
∴△BOC为等腰直角三角形，
由BC=4可知，BO=
.
故答案为：.
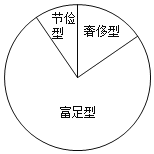
【题目】某校为了解学生零用钱支出情况，从七、八、九年级800名学生中随机抽取部分学生，对他们今年5月份的零用钱支出情况进行调查统计，并绘制成如下统计图表：
组别 | 零用钱支出x（单位：元） | 频数（人数） | 频率 | |
节俭型 | 一 | x＜20 | m | 0.05 |
二 | 20≤x＜30 | 4 | a | |
富足型 | 三 | 30≤x＜40 | n | 0.45 |
四 | 40≤x＜50 | 12 | b | |
奢侈型 | 五 | x≥50 | 4 | c |
合计 | 1 | |||
（1）表中a+b+c＝ ；m＝ ；本次调查共随机抽取了 名同学；
（2）在扇形统计图中，“富足型”对应的扇形的圆心角的度数是 ；
（3）估计今年5月份全校零花钱支出在30≤x＜40范围内的学生人数；
（4）在抽样的“奢侈型”学生中，有2名女生和2名男生．学校团委计划从中随机抽取2名同学参加“绿苗理财计划”活动，请运用树状图或者列表说明恰好抽到一男一女的概率．
